LLM Quantization

이 글은 “Maarten Grootendorst"의 허락을 받고 Visual Guide To Quantization 글을 간결하게 설명하였다.

대형 언어 모델(LLM)은 상용 하드웨어에서 실행하기에는 매우 크다. 이러한 모델은 수십억 개의 파라미터를 보유하며, 일반적으로 추론 속도를 높이기 위해 많은 메모리 용량을 가진 GPU가 필요하다. 따라서 점점 더 많은 연구가 이러한 모델을 더 작게 만드는 것에 초점을 맞추고 있다. 이는 개선된 학습, 어댑터 등의 방법을 통해 이루어집니다. 이 분야에서 주요한 기법 중 하나는 양자화(quantization)라고 부른다.

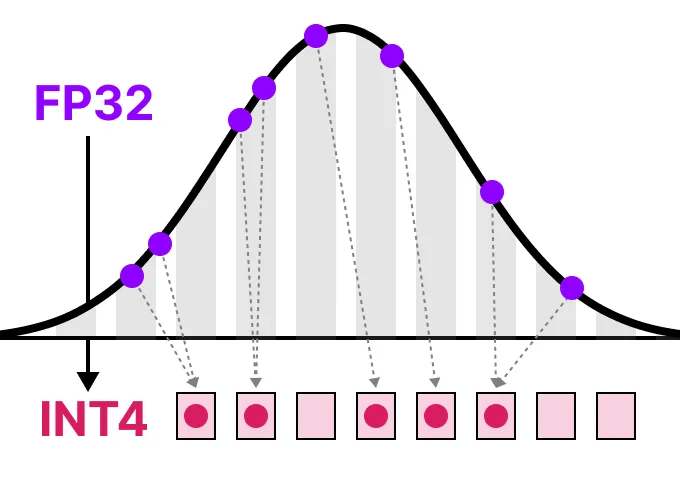
이 포스트에서는 대형 언어 모델을 위한 양자화 분야 기술 갈래와 직관적인 이해를 목표로 한다. 따라서 LLM 양자화를 위한 다양한 방법, 유즈 케이스, 양자화 원리 등을 탐구한다.

LLM의 문제

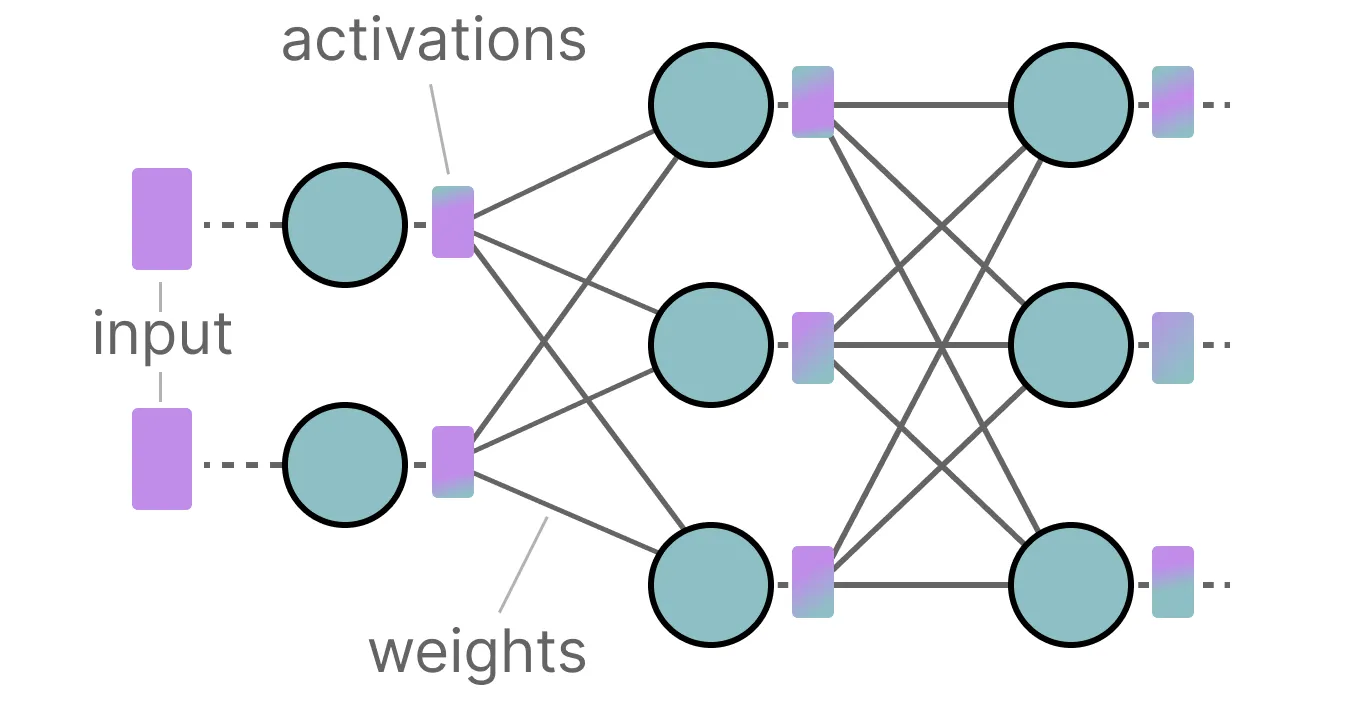
오늘 날 LLM은 매우 많은 파라미터(가중치)를 포함한다. 수십 억 개의 파라미터를 메모리에 한 번에 저장하는 것은 매우 비용이 많이 드는 작업이다. 특히 추론하는 동안, 입력과 가중치 간의 연산으로 활성화 값이 생성되며, 이를 저장하기 위한 메모리 비용도 만만치 않다. 결과적으로 수십 억개의 파라미터를 효율적으로 표현하는 방법은 이 값들을 저장하는 메모리 공간을 최소화하는 것이 중요하다.

컴퓨터가 수치를 표현하는 방법

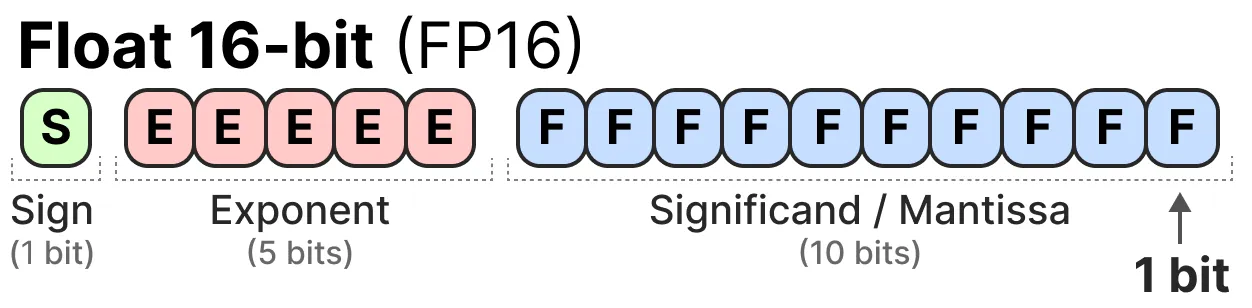
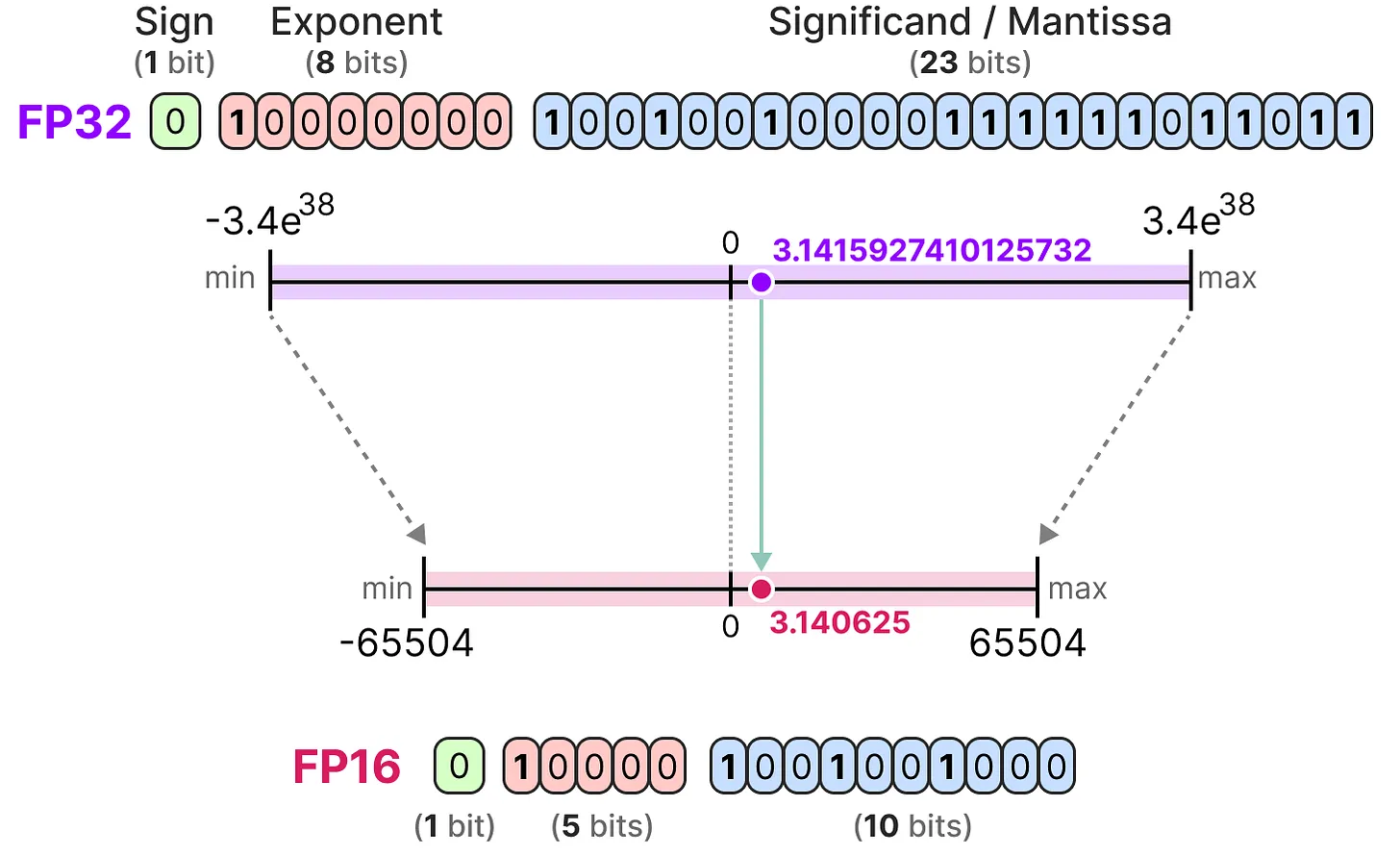
주어진 값은 흔히 소수점이 있는 양수 또는 음수인 부동 소수점 숫자(또는 컴퓨터 과학에서는 부동 소수점)로 표시한다. 이러한 값은 ‘비트’ 또는 2진수로 표시되는데, IEEE-754 표준에서는 비트가 부호, 지수 또는 분수(또는 맨티사)의 세 가지 함수 중 하나를 사용하여 값을 표현하는 방법을 설명한다. 아래 그림은 FP16을 표현하는 국제 표준 방법이다. 맨 앞 1-bit는 부호이고, 그 다음 5-bit는 정수부 또는 지수부이고, 마지막 10-bit는 가수부 또는 맨티사라 부르는 유효 숫자 표기이다.

이제 FP16에서 무리수 phi를 표현하는 예시이다.

더 정밀한 FP32로 무리수 phi를 표현하는 것과의 차이는 아래와 같다.

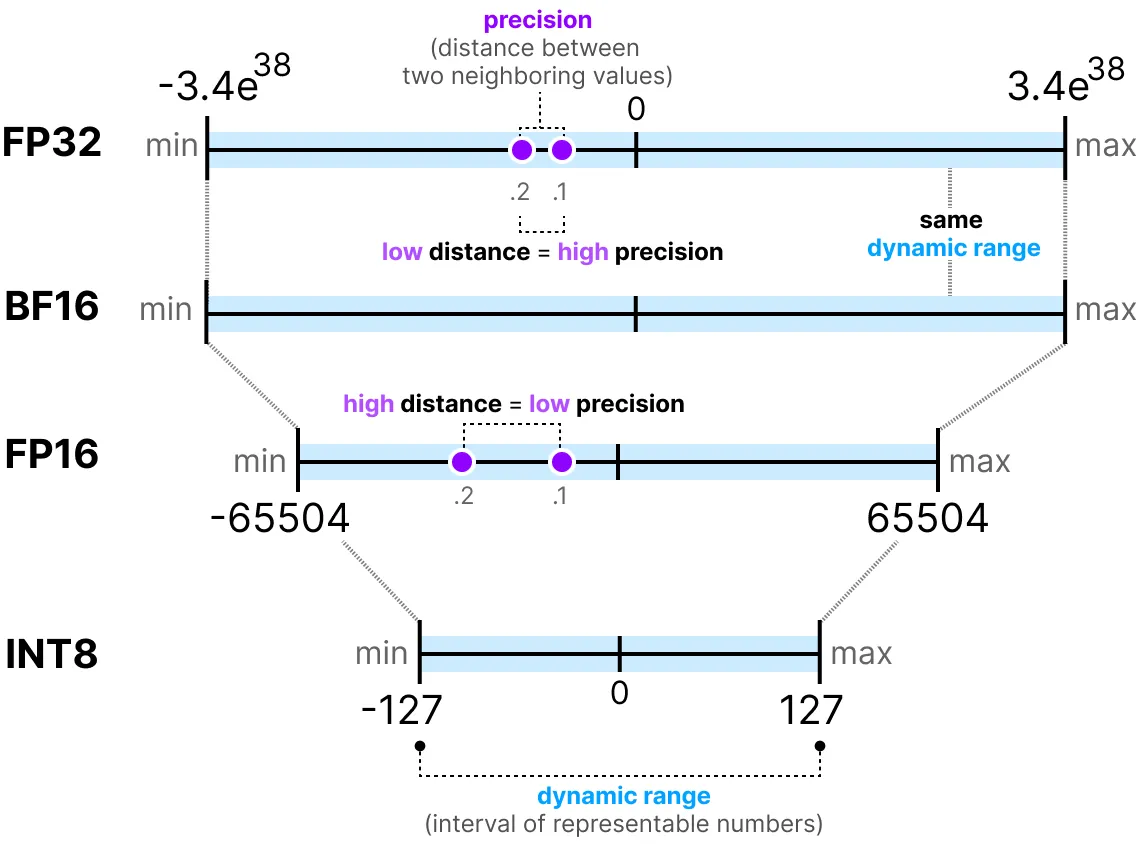
연산 방식에서 알 수 있듯이, 정수부는 데이터 표현의 범위를 결정하고, 가수부는 데이터 표현의 정밀도를 결정한다. 직관적으로 FP32는 FP16보다 더 큰 수를 표현할 수 있지만, 정밀도는 떨어진다. 반면에 FP16는 FP32보다 표현 가능한 수는 제한되지만, 정밀도는 더 높다.

메모리 제약 조건

위의 말을 정리하자면, 어떻게 비트 할당이 가능한지에 따라, 표현할 수 있는 값의 범위가 달라진다.

주어진 데이터형이 표현 가능한 숫자의 간격을 동적 범위(dynamic range)라고 한다. 그리고 이 인접한 두 값 차이를 정밀도(precision)이라고 한다.

이러한 비트의 주요한 기능은 디바이스에서 주어진 값을 저장하기 위한 필요한 메모리의 양을 계산할 수 있다. 예를 들어 1바이트의 메모리에는 8비트가 있으므로 대부분의 부동소수점 표현 형식에 대한 기본 공식을 만들 수 있다.

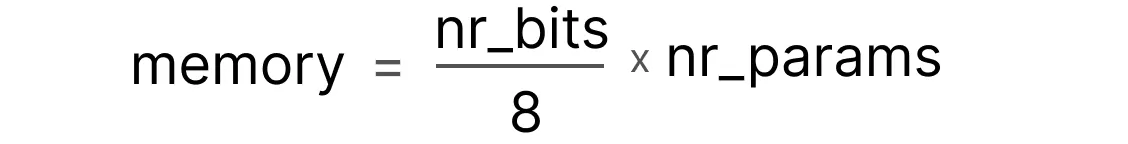
이제 700억 개의 파라미터가 있는 모델이 있다고 가정해본다. 대부분의 모델은 기본적으로 부동 소수점 32비트(흔히 고정밀이라고 함)로 표현되며, 이 경우 모델을 로드하는 데만 280GB의 메모리가 필요하다.

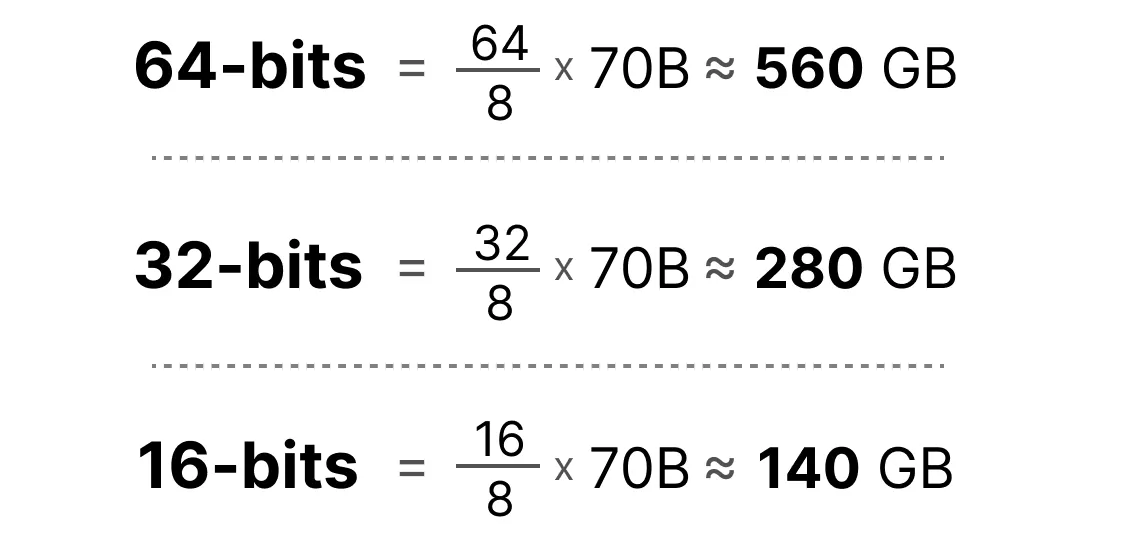
이러힌 이유로 모델 파라미터를 효율적으로 표현하기 위해 비트 수를 낮추는 기술은 매우 중요하다. 그러나 정밀도가 떨어지면 일반적으로 모델의 정확도도 떨어진다. 이 트레이드 오프를 결정하기 위해 양자화 전략이 필요하다.

Introduction of Quantization

양자화는 32비트 부동 소수점처럼 높은 비트 폭에서 8비트 정수와 같은 낮은 비트 폭으로 모델 파라미터 정밀도를 낮추는것을 목표한다.

본디 파라미터를 표현하는 비트 수를 낮추면, 자연스럽게 정밀도가 손실된다. LLM 양자화 뿐만 아니라 전통적으로 이미지 처리에서 색을 표현하는 가짓 수를 8비트로 낮추게 되면, 이미지의 granularity가 거칠어지는 사례가 있다.

사진에서 확대한 부분은 더 적은 색상을 이용하여 이미지를 표현할 수 있다. 더 적은 색상을 이용한다는 것은 원본보다 이미지가 거칠어짐을 의미한다. 이처럼 양자화의 주요 목표는 본래의 파라미터 정밀도를 최대한 보존하면서, 동시에 파라미터를 표현하는데 필요한 비트 수를 줄이는 것에 있다.

Comoon Data Type

FP16

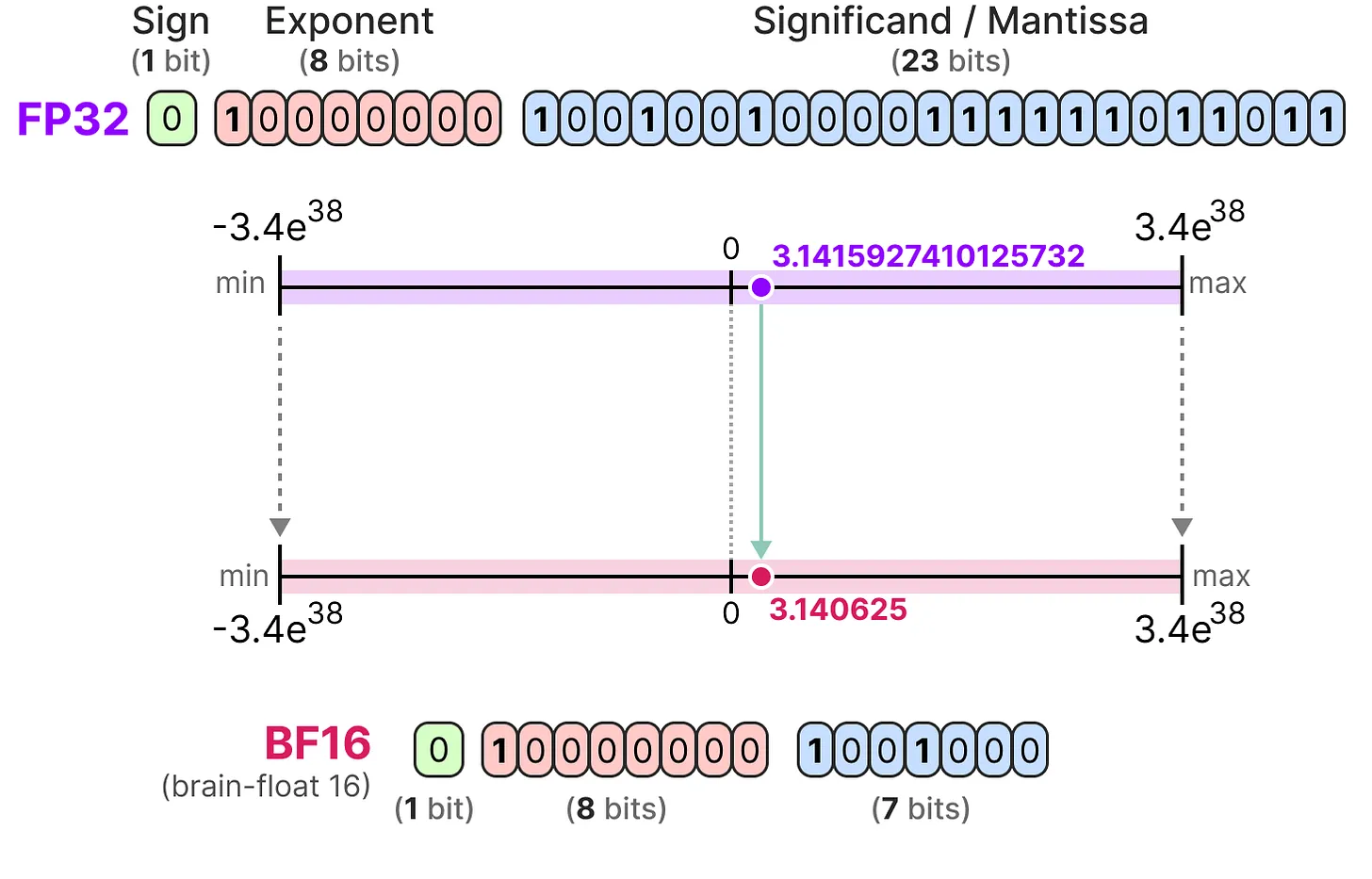
먼저 일반적인 부동 소수점 데이터 유형은 FP32이다. 이를 FP16으로 낮추는 과정을 살펴본다. 이때 FP16이 취할 수 있는 값의 범위가 FP32보다 매우 작은 것에 주목해야 한다. 이러한 단점을 극복하기 위해, FP32와 비슷한 범위를 가질 수 있으면서도 정밀도를 낮춘 BF16이 개발되었다.

BF16

BF16은 FP16과 동일한 비트 수를 사용하지만 더 넓은 범위의 값을 사용할 수 있으며 딥 러닝 애플리케이션에 자주 사용된다.

INT8

비트 수를 더 줄이면 부동 소수점 표현이 아닌 정수 기반 표현의 영역에 접근하게 된다. 예를 들어 FP32를 8비트에 불과한 INT8로 변환하면 원래 비트 수의 4분의 1이 된다.

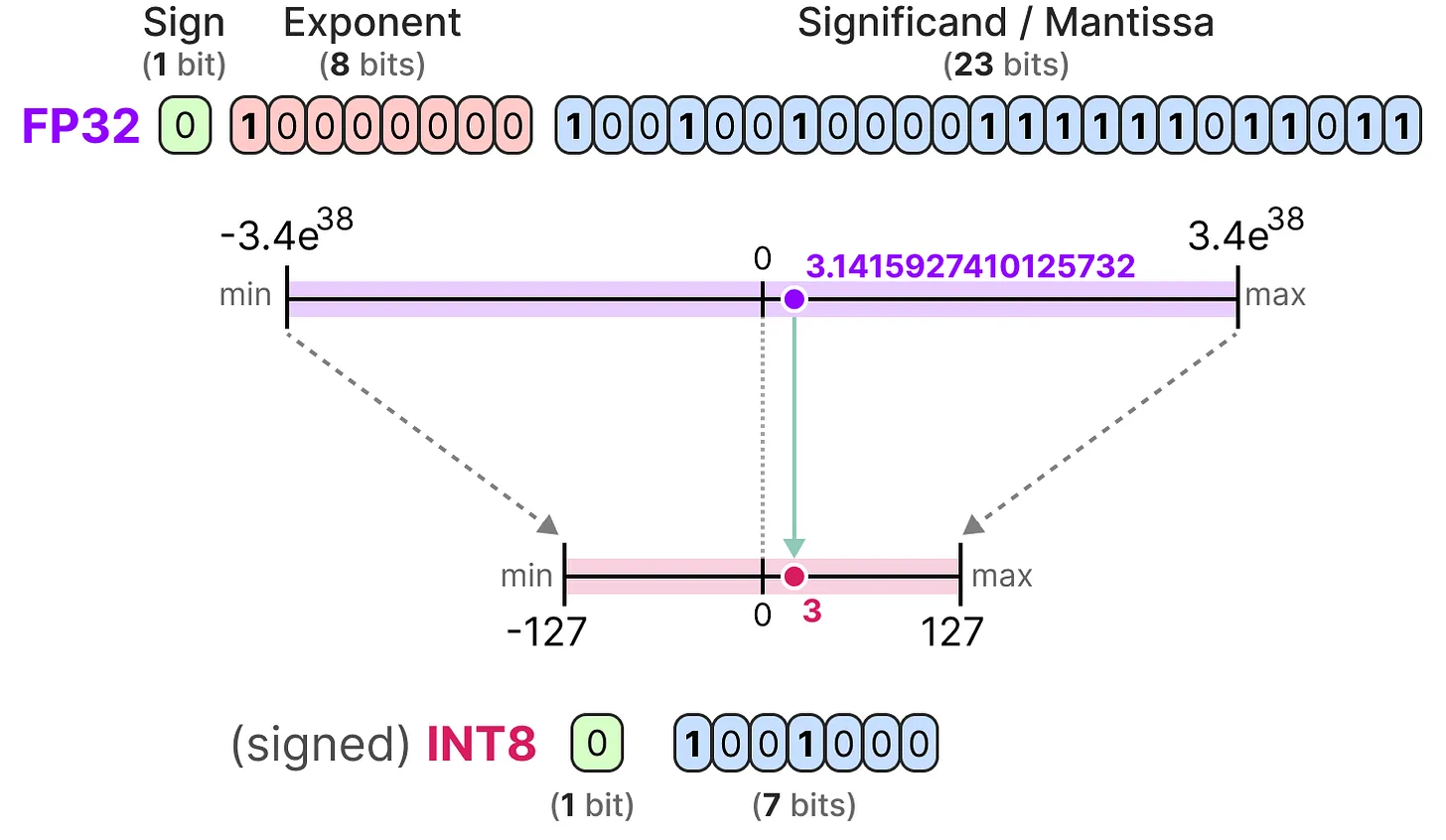
비트가 줄어들 때마다 매핑을 수행하여, 초기 FP32 표현을 더 낮은 비트로 “압축"한다. 실제로는 전체 FP32 범위[-3.4e38, 3.4e38]를 INT8에 매핑할 필요는 없다. 모델 파라미터를 INT8로 매핑하는 방법만 찾으면 된다. 일반적인 스퀴징/매핑 방법은 대칭 및 비대칭 양자화이며 선형 매핑의 한 형태이다. 이러한 방법을 생각하여 FP32에서 INT8로 양자화해본다.

Symmetric Quantization

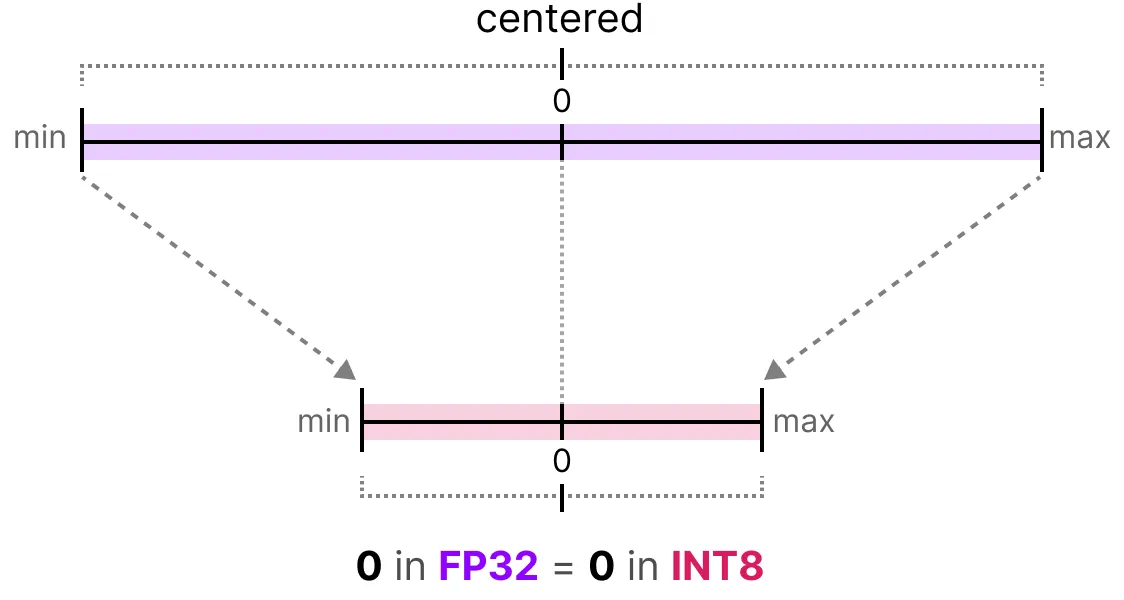
대칭 양자화는 원래 부동 소수점 값의 범위가 양자화된 공간에서 0을 중심으로 한 대칭 범위에 매핑된다. 이전 예제에서 양자화 전후의 범위가 0을 중심으로 유지되는 것을 볼 수 있다. 이는 부동 소수점 공간에서 0에 대한 양자화된 값이 양자화된 공간에서 정확히 0이 되는 것을 의미한다.

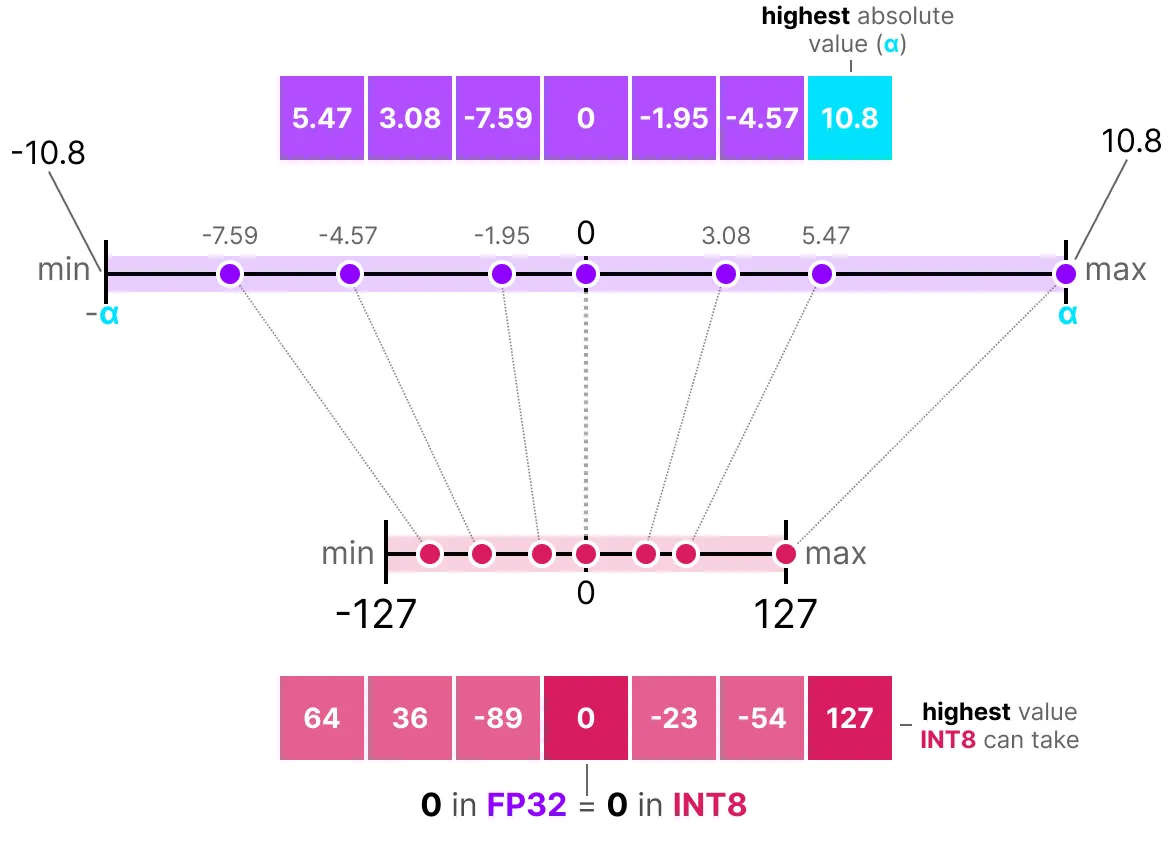
대칭 양자화의 좋은 예로 absmax 양자화를 생각할 수 있다. 값 목록이 주어지면 가장 높은 절대값 alpha를 취하여, 선형 매핑을 수행할 기준으로 정한다.

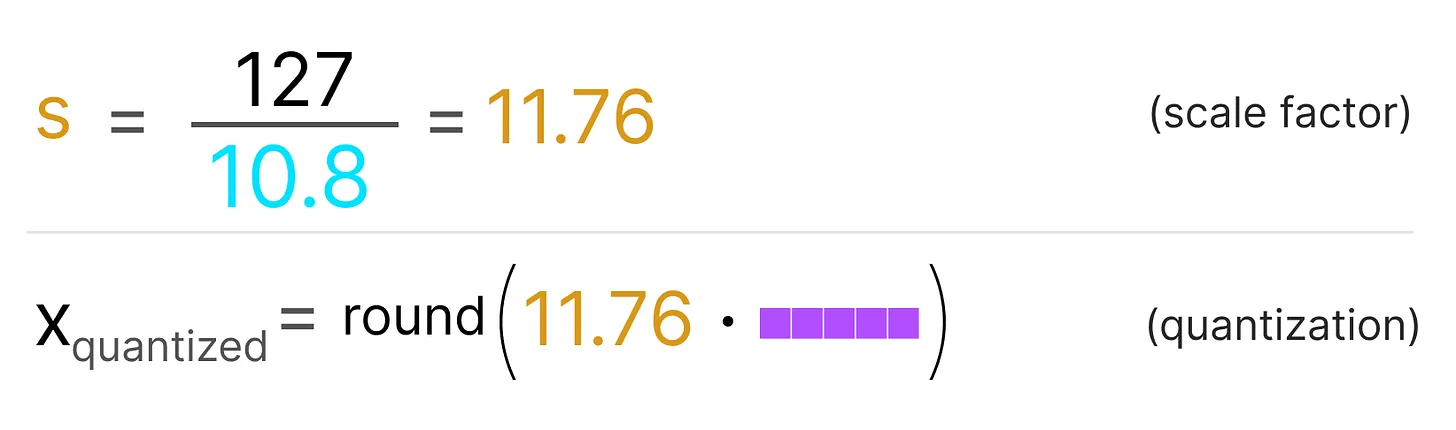
0을 중심으로 한 선형 매핑이므로, 수식은 간단하다.

• b: 양자화를 하기 위한 바이트 수
• a: 가장 큰 절대값

이제 임의의 부동 소수점 입력 x를 양자화할 수 있다.

위 식에 적절한 값을 대입하면,

와 같이 연산할 수 있다.

또한 이전에 활용한 scale factor를 활용하여 양자화된 값을 원래의 FP32 값으로 복원할 수 있다.

양자화 및 비양자화 프로세스를 적용하여 원본을 검색하는 방법은 다음과 같다.

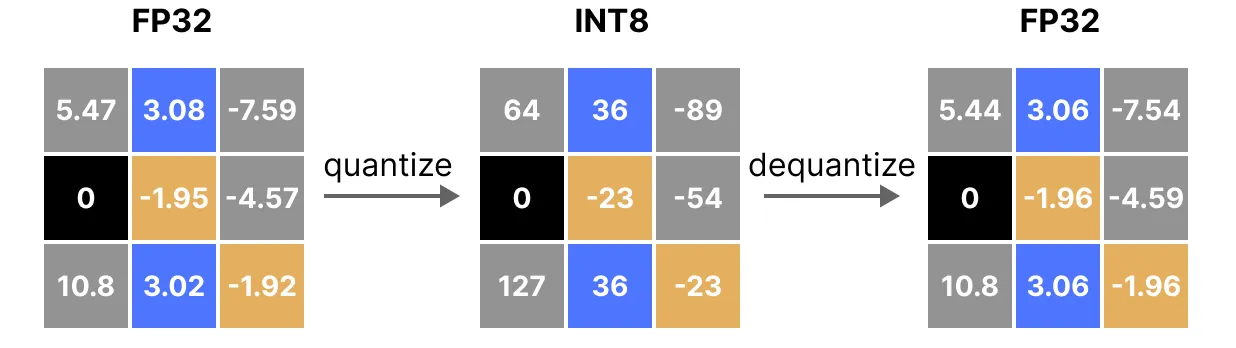
위 그림에서 3.08과 3.02와 같은 특정 값이 INT8, 즉 36에 할당된 것을 볼 수 있다. 값을 양자화하여 FP32로 반환하면 정밀도가 떨어지고 더 이상 구분할 수 없게 된다. 이를 흔히 양자화 오차라고 하며, 원래 값과 양자화된 값의 차이를 구하여 계산할 수 있다.

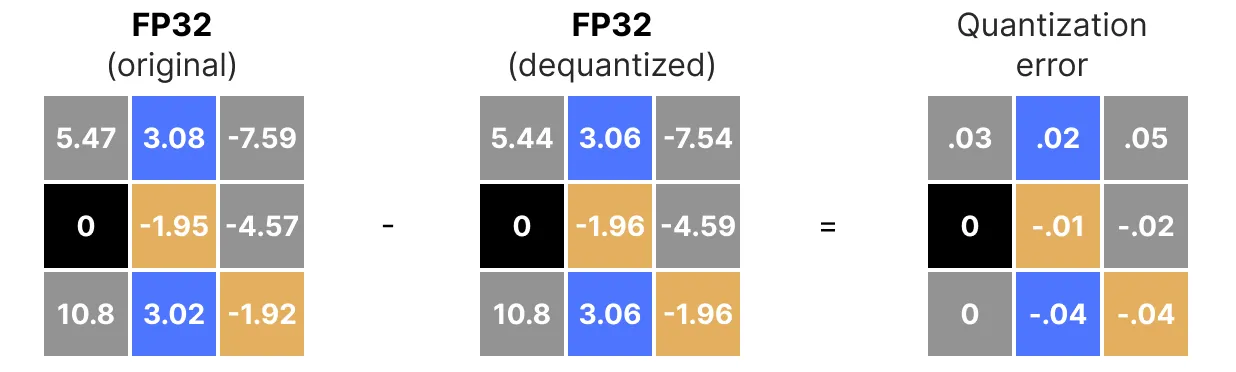
일반적으로 양자화 비트 수가 더 낮을수록, 원래의 정밀도로 복원하는데 발생하는 양자화 차이가 더 크다.

Asymmetric Quantization

반면 aymmtric 양자화는 0을 중심으로 대칭이 아니다. 대신 실수 범위의 최소값(β)과 최대값(α)을 양자화된 범위의 최소값과 최대값에 매핑한다. 이제 살펴볼 방법을 영점 양자화(zero-point quantization)라고 합니다.

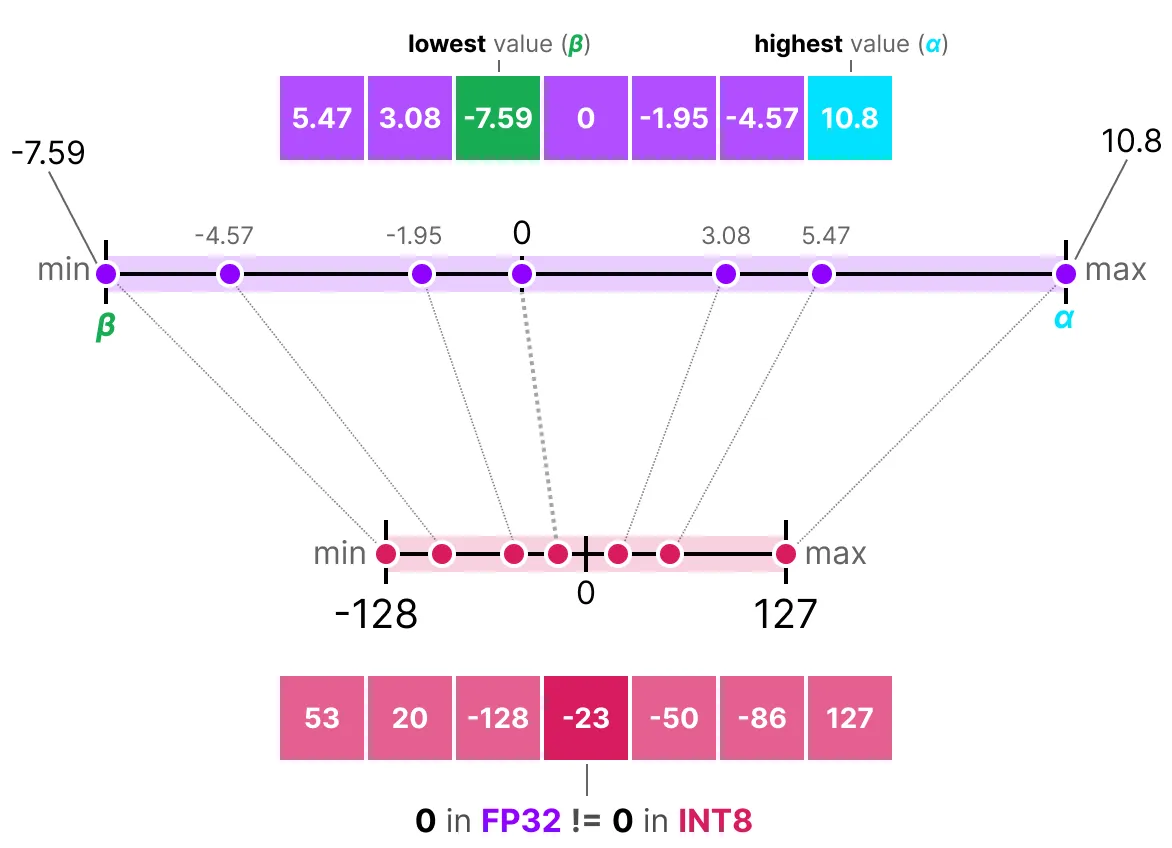
0의 위치가 어떻게 바뀌었는지 확인할 필요가 있다. 이것이 바로 비대칭 양자화라고 불리는 이유이다. 최소/최대 값은 [-7.59, 10.8] 범위에서 0까지의 거리가 다르다. 위치가 바뀌었기 때문에 선형 매핑을 수행하려면 INT8 범위의 영점을 계산해야 한다. 이전과 마찬가지로 scale factor도 계산해야 하지만 대신 INT8 범위의 차이[-128, 127]를 사용한다.

파라미터를 이동하기 위해, INT8 범위에서 영점을 계산해야 한다. 따라서 조금 더 복잡한 수식이 된다. 이전과 마찬가지로 수식을 서술하고 적절한 값을 대입해본다.

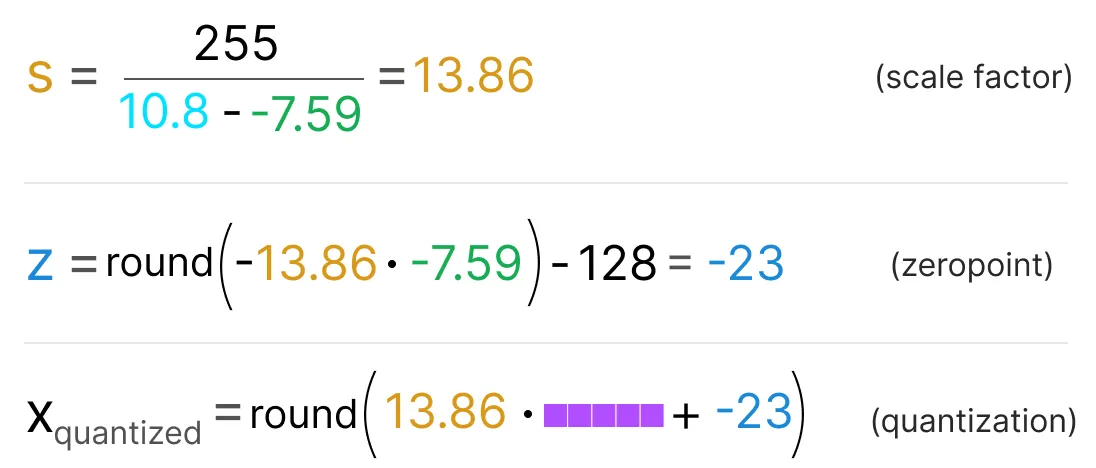
이 수식에서 INT8를 FP32로 복원하기 위해서는, 이전에 계산하였던 scale factor와 zero-point가 필요하다. 다시 말해, dequantization 과정은 아래처럼 쓸 수 있다.

지금까지 대칭, 비대칭 양자화를 살펴보았다. 두 과정을 비교하면 아래의 결론이 나온다.

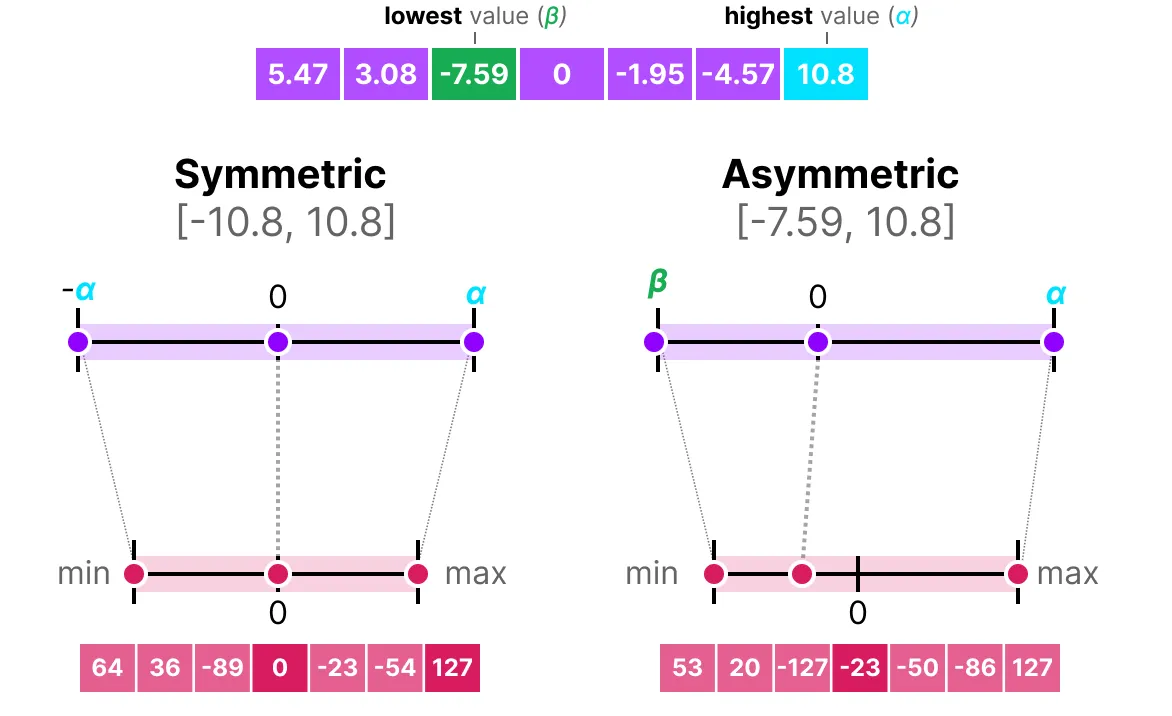
특히, 대칭 양자화의 zero-centered 특성과 비대칭 양자화의 오프셋에 주목한다.

매핑과 클리핑 범위

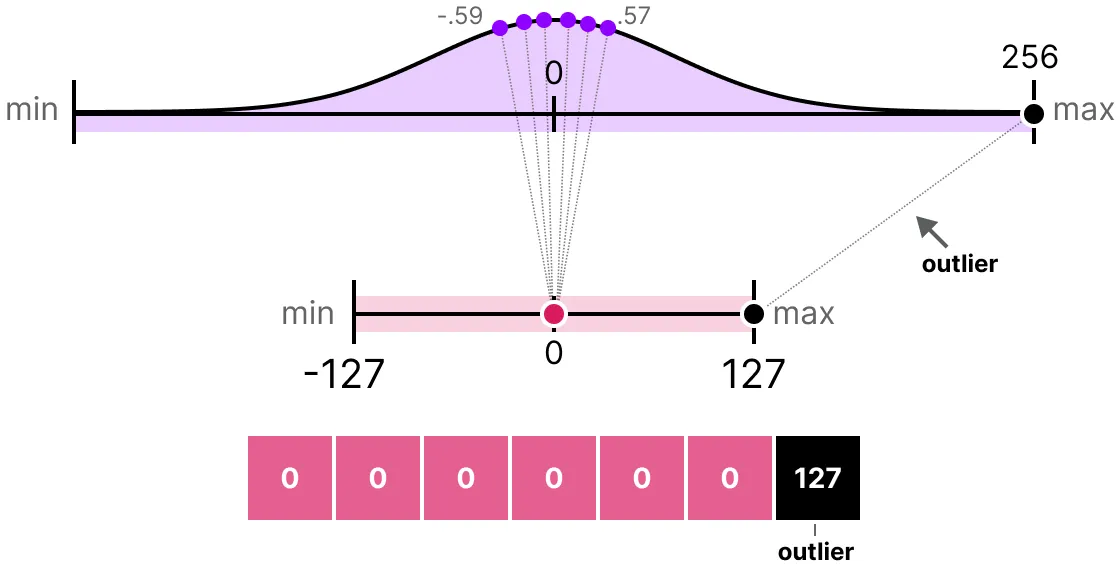
이전 예제에서는 주어진 파라미터 범위를 더 낮은 비트 표현으로 매핑하는 방법을 살펴보았다. 이 방법은 파라미터의 전 범위를 정해진 규칙에 따라서 매핑할 수 있지만, 이상치가 분포하는 파라미터 범위에서는 좋은 방법이 아니다.

아래의 그림 예시에서 그 현상을 살펴볼 수 있다. 파라미터 분포의 양 끝에서 이상치 값이 얕게 퍼져있으면, 양자화 시, 중간값 주변의 값들은 모조리 0으로 매핑되는 결과가 발생한다. 이는 원본 파라미터 분포의 성질을 반영하는 양자화가 아니다.

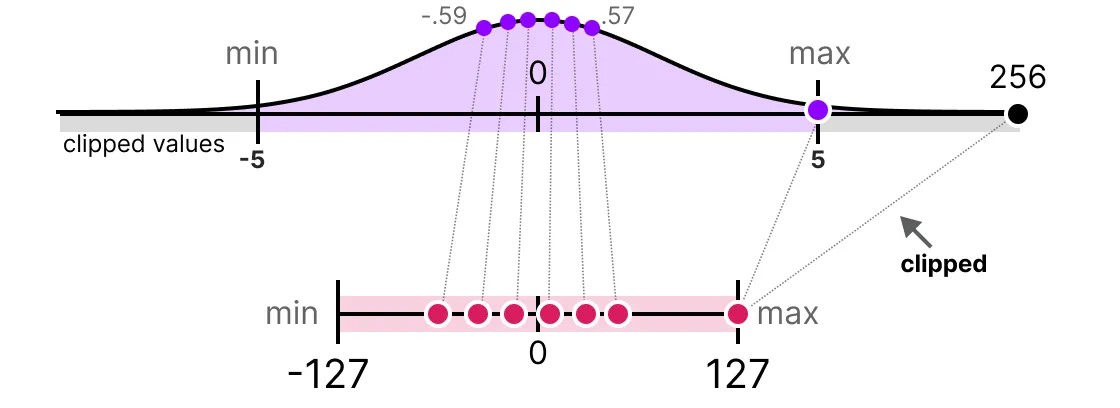
대신에 특정 값을 clipping하여, 이 문제를 해결할 수 있다. clipping은 모든 이상값이 동일한 값을 갖도록, 원본 파라미터들의 동적 범위(Dynamic Range)를 다르게 설정하는 것이다. 아래 예시에서 동적 범위를 [-5, 5]로 설정하면, 원본 파라미터에서 이 범위 밖의 이상치들은 모두 -127 또는 127에 매핑된다. 이 방법의 주요한 이점은 이상치가 아닌 값에 의한 양자화 오차가 줄어든다. 반면에 이상치에 의한 양자화 오차는 증가한다.

Calibration

보정(calibration)은 양자화 오차를 최소화하면서, 위에서 언급한 동적 범위를 적절하게 선택하기 위한 방법이다. 따라서 양자화 오차를 최소화하며 동시에 가능한 많은 파라미터를 포함하는 범위를 찾는 것을 목표한다. 보정은 모든 파라미터에 동일한 기준으로 적용이 안될 수도 있다.

Weight and Biases

LLM의 가중치와 바이어스는 모델을 실행하기 전에 이미 스토리지에 저장되어 있으므로, static하다고 볼 수 있다. 예를 들어 20GB에 달하는 Llama 3의 체크포인트는 대부분 가중치와 바이어스로 구성되어 있다.

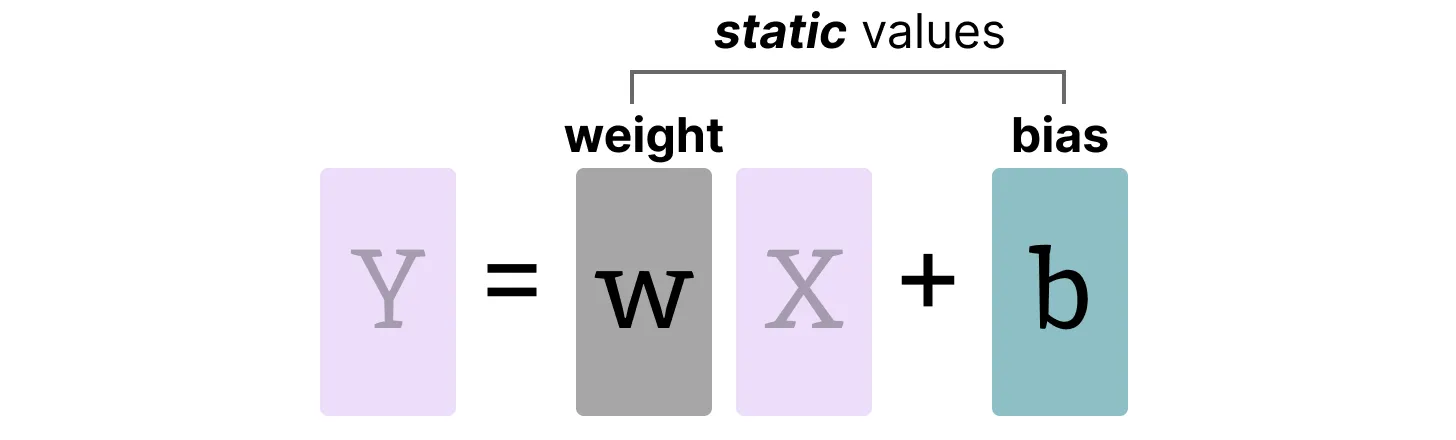
가중치(수십억)보다 바이어스(수백만)가 훨씬 적기 때문에, 바이어스는 종종 더 높은 정밀도(예: INT16)로 유지되며, 양자화는 주로 가중치에 적용한다. static 가중치의 경우, 범위를 선택하는 보정 방법은 다음과 같다.

• 입력 범위의 백분위 수를 수동으로 선택
• 원본 가중치와 양자화된 가중치 사이의 평균 제곱 오차(MSE)
• 원본 가중치와 양자화된 가중치 사이의 엔트로피(KL-차이 최소화하기) 최적화

예를 들어 백분위 수를 선택하면, 앞서 본 것처럼 clipping 비슷한 동작이 발생한다.

Activations

LLM 전체에서 지속적으로 업데이트되는 입력 값은 일반적으로 활성화 값(activation)이라고 불린다. 이 값들은 종종 시그모이드(sigmoid)나 렐루(ReLU)와 같은 활성화 함수(activation function)를 거치기 때문에 활성화 값이라고 불린다. 가중치와 달리 활성화 값은 추론(inference) 중에 모델에 입력 데이터가 들어올 때마다 변하기 때문에 정확하게 양자화하기가 어렵다.

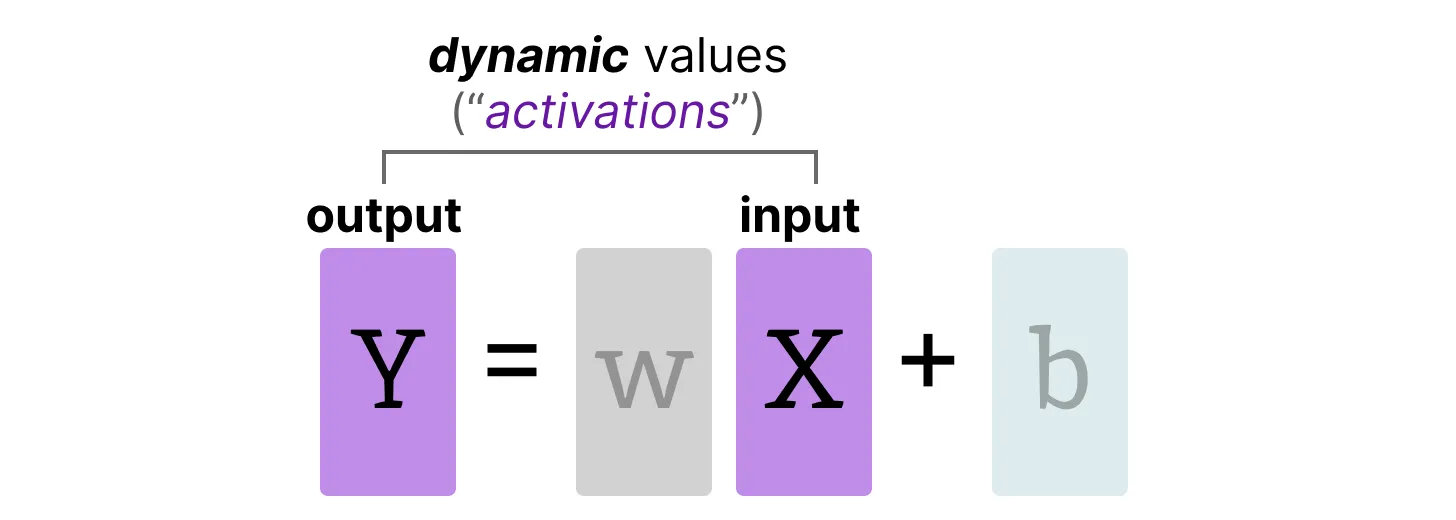
이 값들은 각 은닉 층을 통과한 후에 업데이트되므로, 입력 데이터가 모델을 통과하는 동안에만 이 값들이 어떻게 될지 알 수 있다.

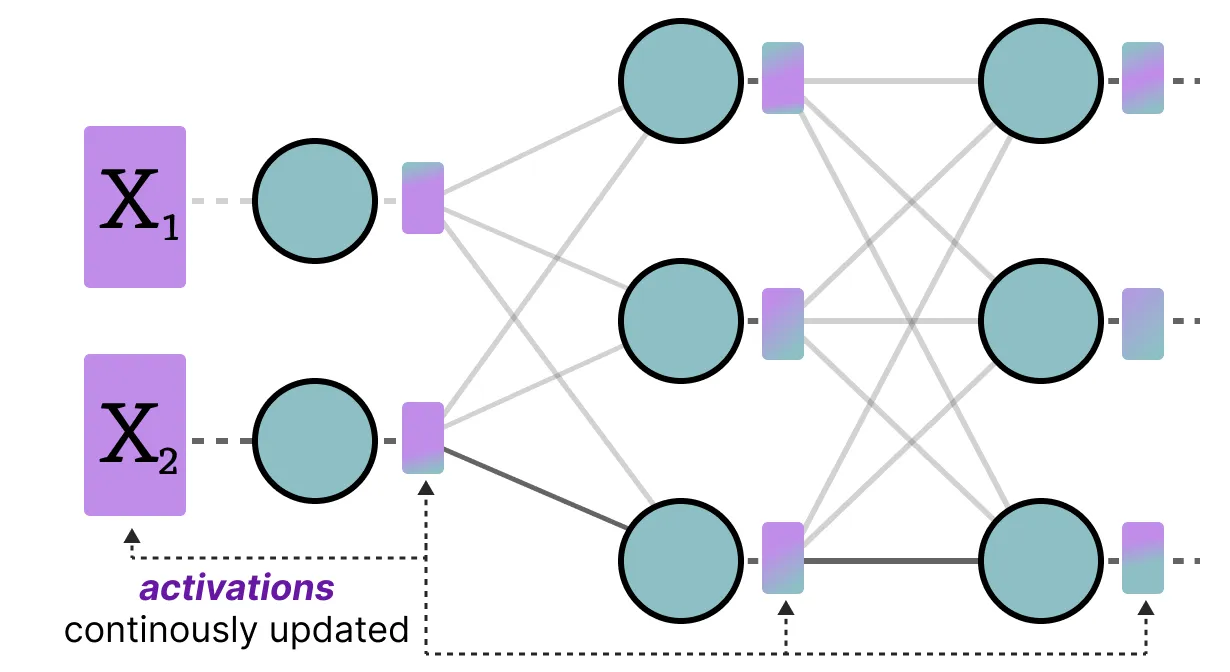
대체로 가중치와 활성화 값의 양자화 방법을 보정하는 두 가지 주요 방법이 있다.

• 훈련 후 양자화 (Post-Training Quantization, PTQ): 훈련 후에 양자화 수행
• 양자화 인지 훈련 (Quantization Aware Training, QAT): 훈련 또는 미세 조정(fine-tuning) 중에 양자화 수행

Post-Training Quantization

가장 널리 사용되는 양자화 기법 중 하나는 훈련 후 양자화(Post-Training Quantization, PTQ)이다. 이는 모델을 훈련한 후에 모델의 매개변수(가중치와 활성화 값)를 양자화하는 것을 포함한다. 가중치의 양자화는 대칭 양자화(symmetric quantization) 또는 비대칭 양자화(asymmetric quantization)를 사용하여 수행된다. 반면, 활성화 값의 양자화는 그 범위를 알 수 없기 때문에 잠재적인 분포를 얻기 위해 모델의 추론이 필요하다.

활성화 값의 양자화에는 두 가지 형태가 있다.

• 동적 양자화 (Dynamic Quantization)
• 정적 양자화 (Static Quantization)

Dynamic Quantization

데이터 은닉 층을 통과할 때마다 각 활성화 값들을 저장한다.

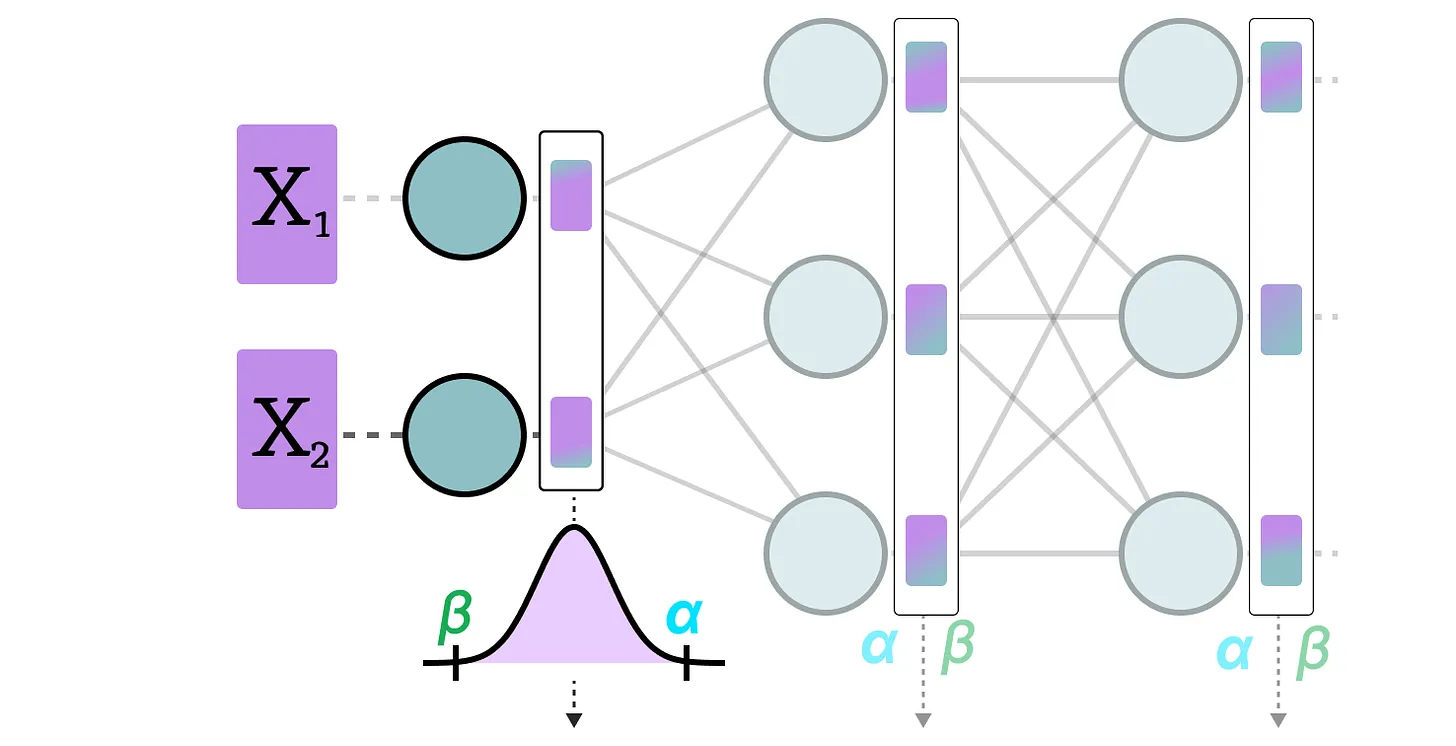
이 활성화 값들의 분포로 zero-point와 scale factor를 연산하여, 양자화에 사용할 수 있다.

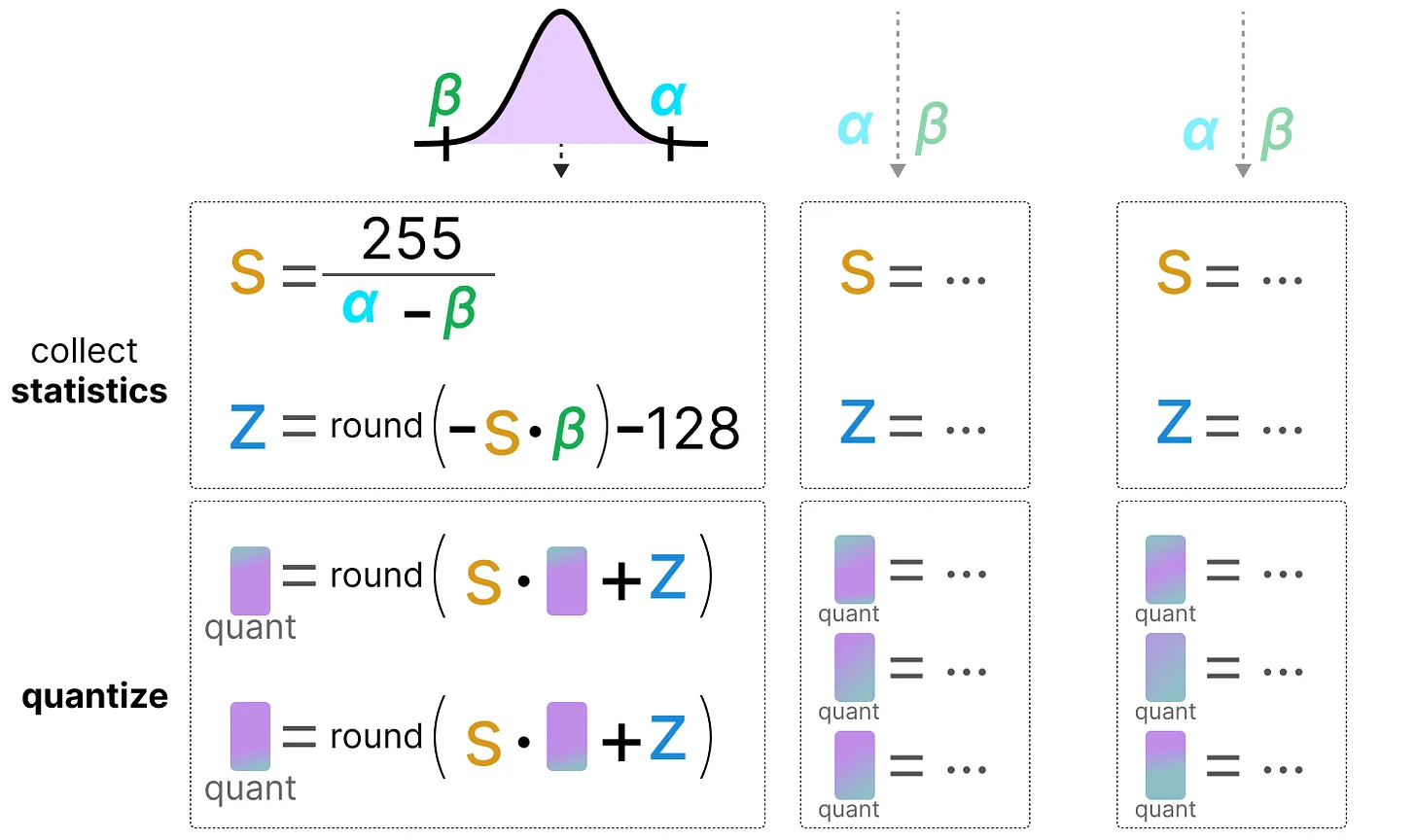
이 과정은 데이터가 새로운 레이어를 통과할 때마다 반복된다. 따라서 각 레이어는 고유한 zero-point와 scale-factor를 가진다. 이에 따라 각 레이어들은 각기 최적화된 양자화 전략을 가져갈 수 있다.

Static Quantization

동적 양자화와 달리, 정적 양자화는 추론 중에 zero-point, scale factor를 계산하지 않고, 미리 계산한다. 이 값들을 찾기 위해 보정 데이터셋(calibration dataset)이 필요하며, 이 데이터셋을 모델에 제공하여 잠재 분포를 추정한다.

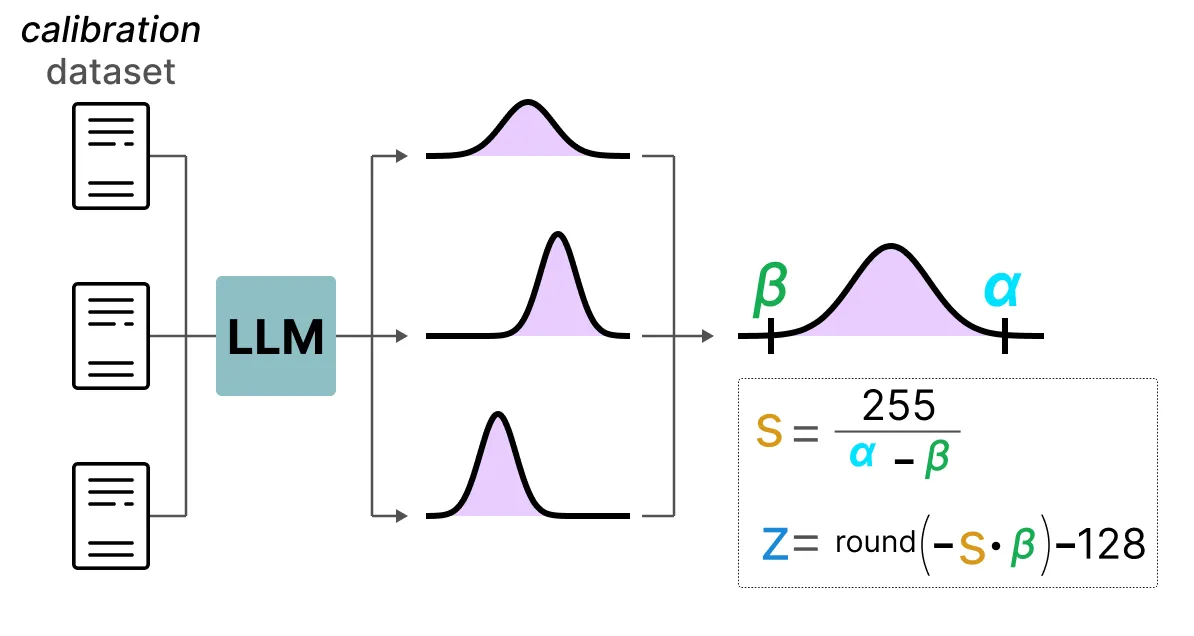
이 값들이 수집된 후, 추론 중에 양자화를 수행하기 위해 필요한 s값과 z값을 계산할 수 있다. 실제 추론을 수행할 때는 s값과 z값이 다시 계산되지 않고, 모든 활성화 값에 대해 전역적으로 사용되어 이를 양자화한다. 일반적으로, 동적 양자화는 각 은닉층마다 s값과 z값을 계산하려고 시도하기 때문에 더 정확한 경향이 있다. 그러나 이러한 값들을 계산해야 하기 때문에 연산 시간이 늘어날 수 있다. 반면, 정적 양자화는 이미 양자화에 사용할 s값과 z값을 알고 있기 때문에 덜 정확하지만 더 빠르다.

4bit 양자화를 향하여

8비트 이하로 양자화하는 것은 양자화 오류가 비트가 줄어들수록 증가하기 때문에 어려운 문제이다. 다행히도, 비트를 6, 4, 심지어 2비트로 줄이는 몇 가지 스마트한 방법이 있습니다. (그러나 이러한 방법을 사용하여 4비트 이하로 줄이는 것은 일반적으로 권장되지 않는다.)

흔히 HuggingFace에서 공유되는 두 가지 방법이 있다.

• GPTQ (GPU에서 전체 모델 실행)
• GGUF (레이어를 CPU로 오프로드할 가능성 있음)

GPTQ

GPTQ는 4비트 양자화를 적용할 수 있는 잘 알려진 방법 중 하나이다. 이 기법은 비대칭 양자화를 사용하며, 각 레이어별로 독립적으로 양자화를 적용한다.

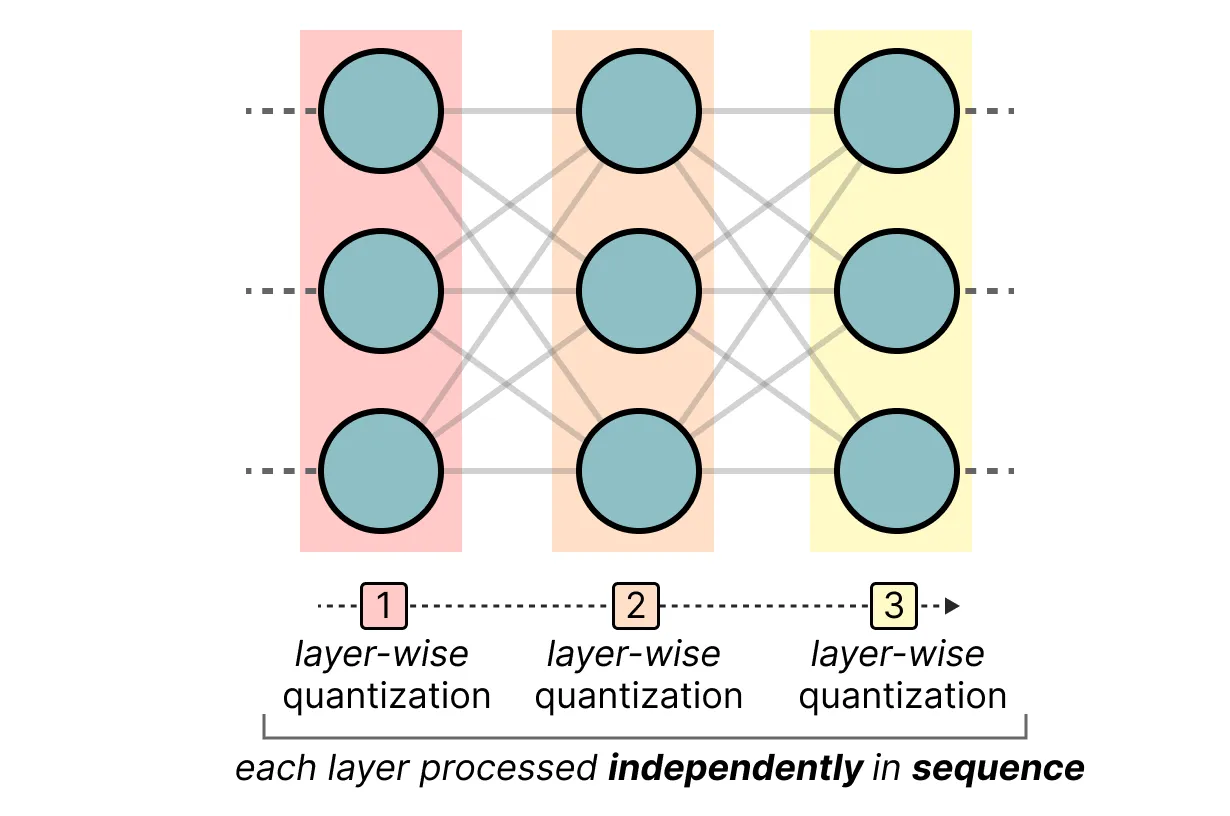
이 레이어별 양자화 과정은 먼저 레이어의 가중치를 inverse-hessian으로 변환한다. inverse-hessian은 모델 손실에 대한 2차 미분이며, 각 가중치 변화에 대해 모델 출력이 얼마나 민감한지의 정보를 담고 있다. 본질적으로 레이어마다, 레이어별 가중치의 중요성을 설명한다. 특히 헤시안 행렬에서 작은 값과 연관된 가중치들은 더 중요한데, 이는 가중치의 작은 변화가 모델 성능에 큰 영향을 미칠 수 있기 때문이다.

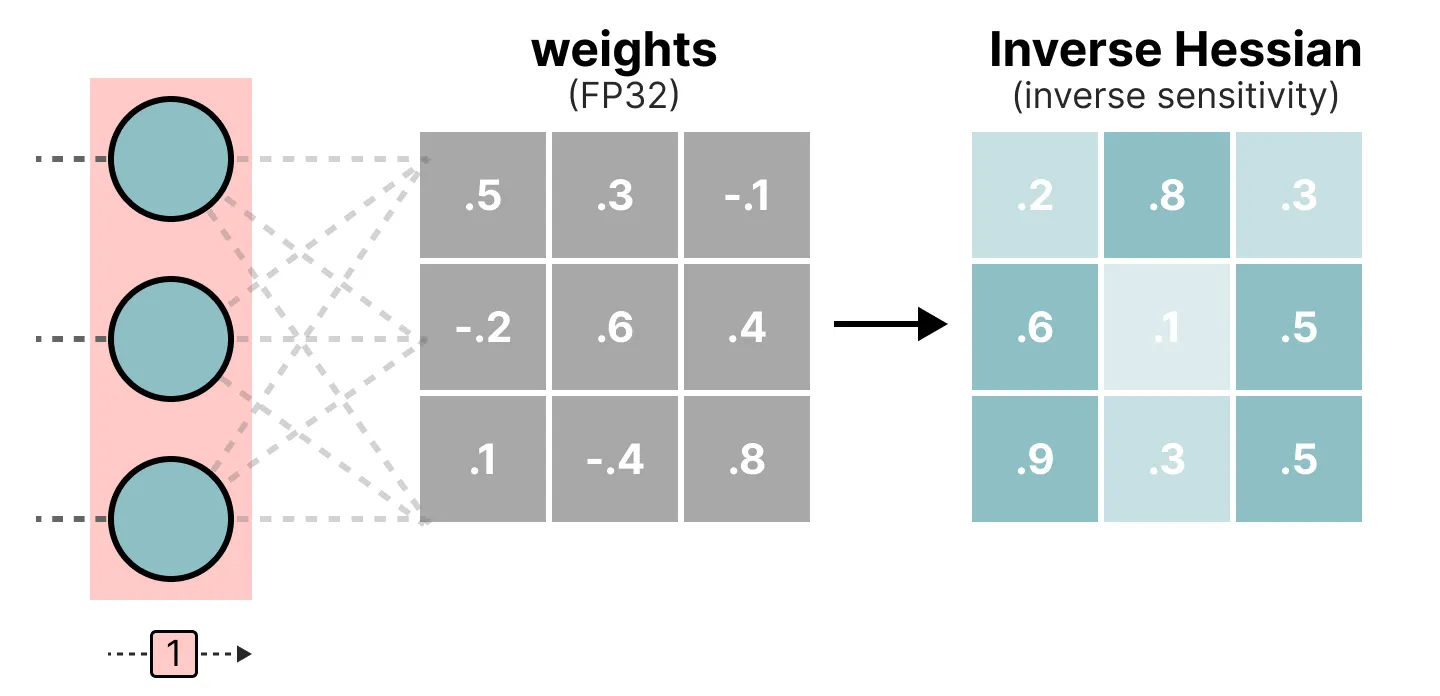
다음으로 가중치 행렬의 첫 번째 행을 quantization한 다음, 다시 dequantization을 한다.

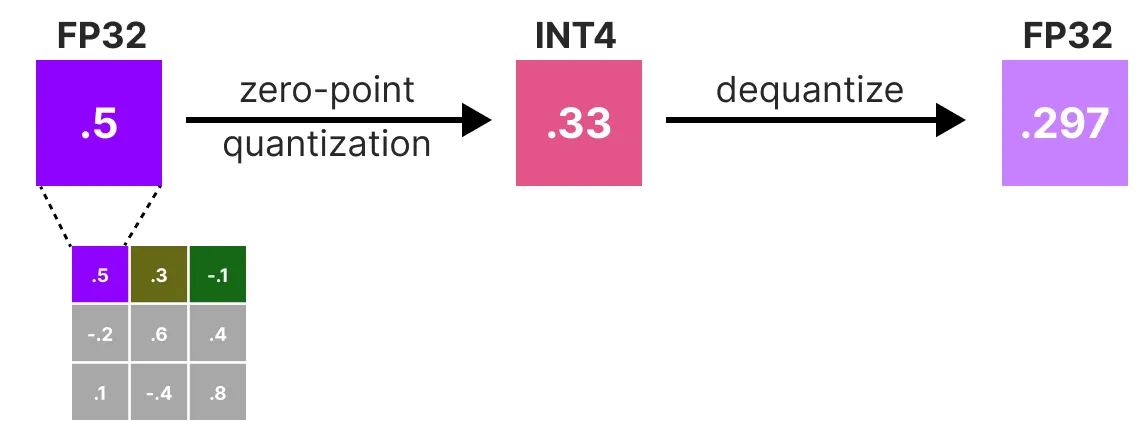
이 과정은 양자화 오류(q)를 계산할 수 있게 해주며, 이는 사전에 계산된 역헤시안(h_1)을 사용해 가중치화할 수 있다. 본질적으로, 가중치의 중요도에 기반한 가중 양자화 오류를 생성하는 것이다.

이제 이 가중된 양자화 오류를 행에 있는 다른 가중치들에 재분배한다. 이를 통해 네트워크의 전체 출력을 유지할 수 있다. 예를 들어, 두 번째 가중치인 0.3 (x_2)에 대해 이 작업을 수행한다고 가정하면, 양자화 오류(q)에 두 번째 가중치의 역헤시안(h_2)을 곱한 값을 추가한다.

우리는 주어진 행에서 세 번째 가중치에 대해서도 동일한 과정을 수행할 수 있다.

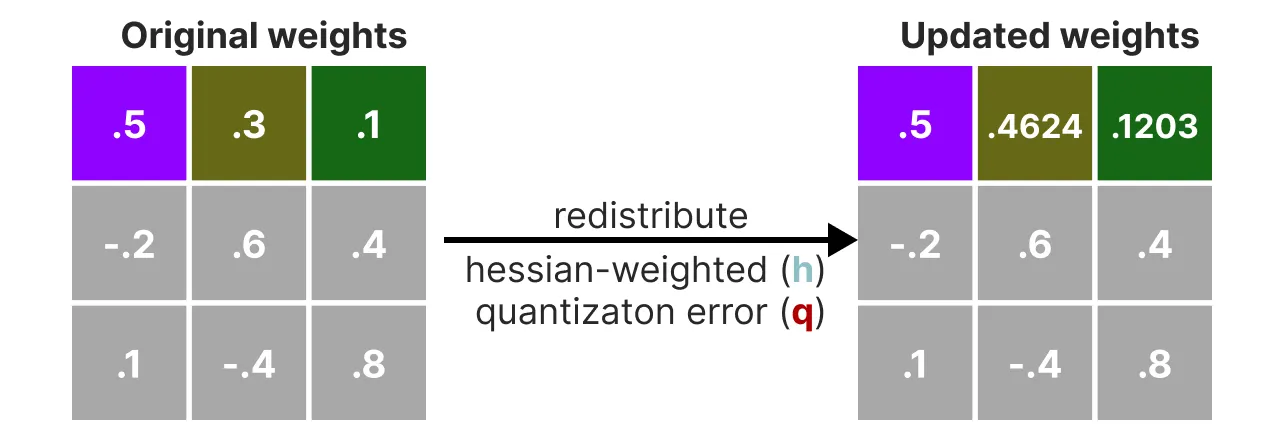
이 가중 양자화 오류를 재분배하는 과정을 반복하여 모든 값을 양자화할 때까지 진행한다. 이 방법이 효과적인 이유는 가중치들이 일반적으로 서로 연관되어 있기 때문이다. 그래서 한 가중치에 양자화 오류가 발생하면, 관련된 가중치들이 역헤시안(inverse-Hessian)을 통해 그에 맞게 업데이트된다.

참고: 저자들은 계산 속도를 높이고 성능을 향상시키기 위해 여러 가지 트릭을 사용했다. 예를 들어, 헤시안에 감쇠 계수(dampening factor)를 추가하고, “레이지 배칭(lazy batching)“을 사용하며, 콜레스키(Cholesky) 방법을 사용해 사전 계산을 수행하는 등의 방법이 있다. 이 주제에 대해 자세히 알고 싶다면 YouTube 영상을 참고할 것을 추천한다.

팁: 성능 최적화 및 추론 속도 향상을 목표로 하는 양자화 방법을 원한다면 EXL2도 있다.

GGUF

GPTQ는 LLM 전체를 GPU에서 실행하기 위한 좋은 양자화 방법이지만, 항상 충분한 GPU 메모리가 있을 수는 없다. 이때는 CPU에서 오프로딩하는 것이 방법일 수 있다. GGUF를 사용한다면 LLM의 특정 레이어를 CPU로 추론 가능하다. 이 방법을 결합하면 VRAM이 충분하지 않을때, CPU와 GPU를 모두 사용할 수 있다.

GGUF 양자화 방법은 자주 업데이트되며, 양자화 비트 수준에 따라 달라질 수 있다. 그러나 일반적인 원칙은 다음과 같다.

주어진 레이어의 가중치를 “슈퍼(super)” 블록으로 나누고, 각 블록에는 여러 개의 “서브(sub)” 블록이 포함됩니다. 이 블록들에서 스케일 팩터(s)와 알파(α)를 추출한다.

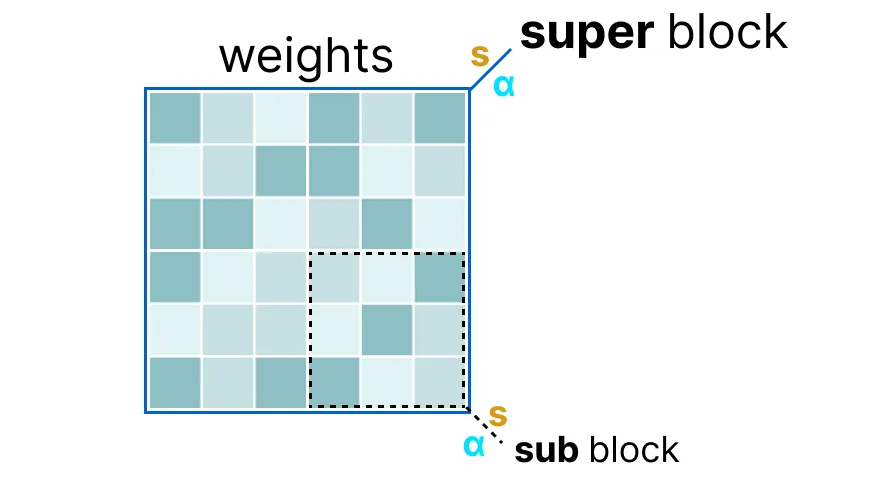
주어진 “서브” 블록을 양자화하기 위해 이전에 사용한 absmax 양자화를 사용할 수 있다. 이 방법은 주어진 가중치에 스케일 팩터(s)를 곱한다.

스케일 팩터는 “서브” 블록의 정보로 계산되지만, 자체 스케일 팩터를 가진 “슈퍼” 블록의 정보를 사용해 양자화된다.

이 블록 단위의 양자화에서는 “슈퍼” 블록의 스케일 팩터(s_super)를 사용해 “서브” 블록의 스케일 팩터(s_sub)를 양자화한다.

각 스케일 팩터의 양자화 수준은 다를 수 있으며, 일반적으로 “슈퍼” 블록의 스케일 팩터가 “서브” 블록의 스케일 팩터보다 더 높은 정밀도를 가진다.

예를 들어, 몇 가지 양자화 수준(2비트, 4비트, 6비트)을 고려할 수 있다.

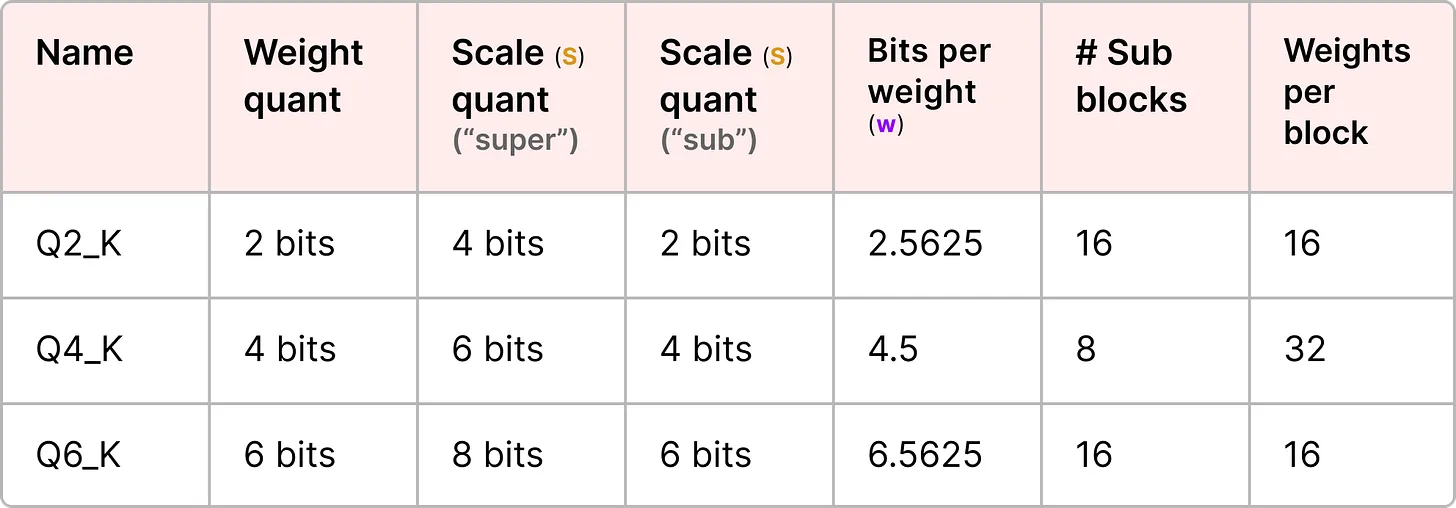
참고: 양자화 유형에 따라 zero-point를 조정하기 위해 추가적인 최소값(m)이 필요할 수 있다. 이 값들은 스케일 팩터(s)와 동일하게 양자화된다. 추가로 아래의 리퀘스트를 참고하면 좋다.

• https://github.com/ggerganov/llama.cpp/pull/1684
• https://github.com/ggerganov/llama.cpp/pull/4861

Quantization-Aware Training

지금까지 살펴본 Post-Training Quantization 방법의 단점은 실제 훈련 과정을 고려하지 않는다는 점이다. 이러한 문제를 해결하기 위해 **양자화 인지 훈련(Quantization Aware Training, QAT)**이 도입된다. QAT는 훈련 후에 모델을 양자화하는 훈련 후 양자화(PTQ)와 달리, 훈련 중에 양자화 절차를 학습하는 것을 목표로 한다.

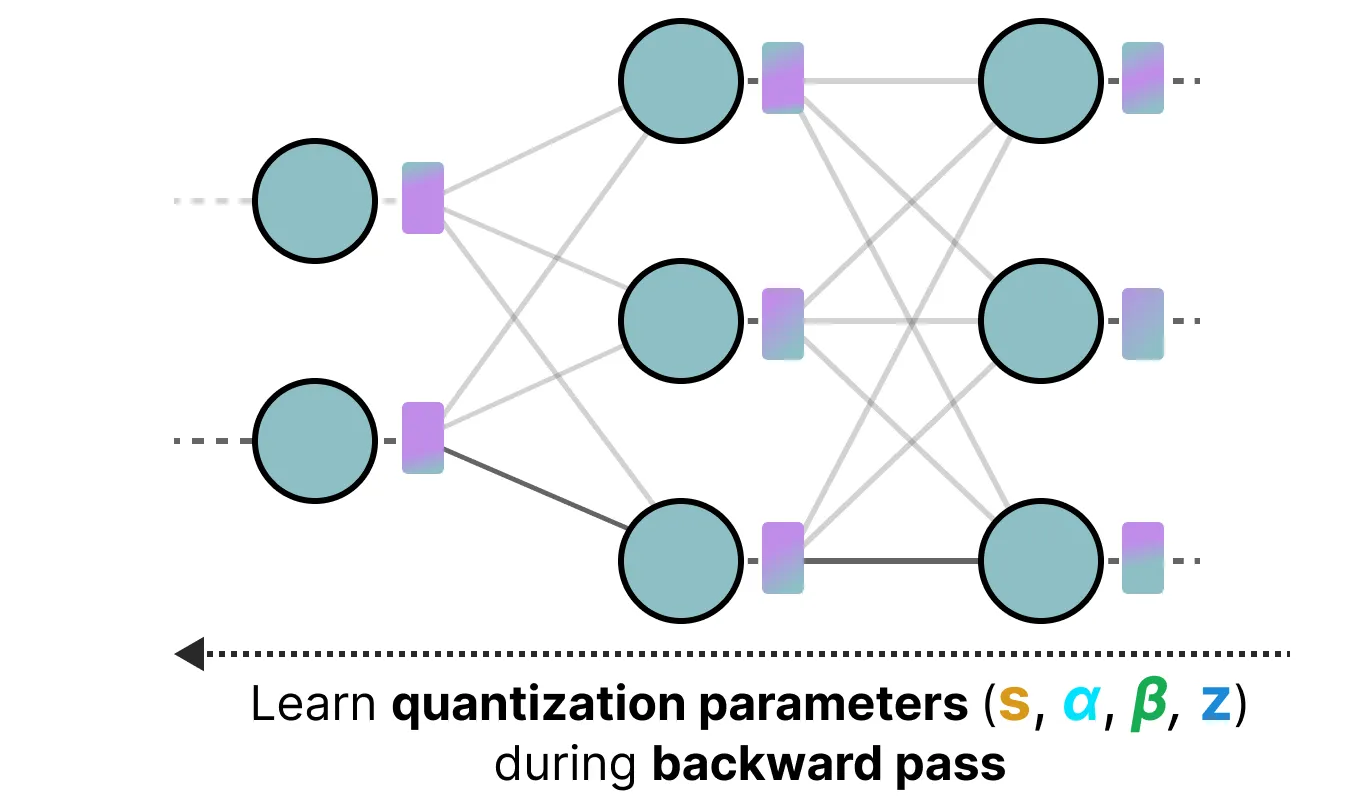
QAT는 훈련 중에 양자화를 고려하기 때문에 PTQ보다 더 정확한 경향이 있다. QAT는 다음과 같이 작동한다. 훈련 중에 “가짜(fake)” quantization이 도입된다. 이는 가중치를 먼저 INT4와 같은 낮은 정밀도로 양자화한 후, 다시 FP32로 dequantization는 과정이다:

이 과정을 통해 모델은 훈련 중에 양자화 과정을 고려하게 되며, 손실 계산과 가중치 업데이트도 함께 이루어진다. QAT는 양자화 오류를 최소화하기 위해 “넓은” 최소점을 탐색하려고 시도한다. 왜냐하면 “좁은” 최소점은 더 큰 양자화 오류를 초래할 가능성이 있기 때문이다.

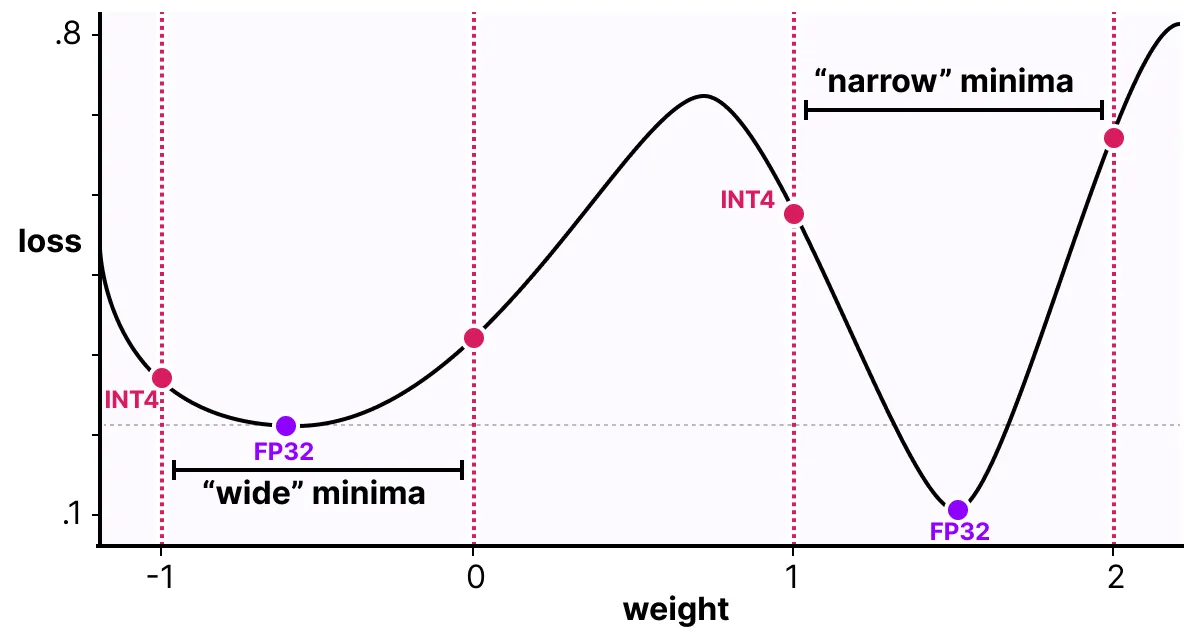
예를 들어, 역전파 중에 양자화를 고려하지 않았다고 가정해 볼 수 있다. 경사 하강법에 따라 가장 작은 손실을 가진 가중치를 선택한다. 그러나 그 가중치가 “좁은” 최소점에 위치해 있다면, 더 큰 양자화 오류가 발생할 수 있다. 반면에, 양자화를 고려하면, 양자화 오류가 훨씬 적은 “넓은” 최소점에서 다른 업데이트된 가중치를 선택한다.

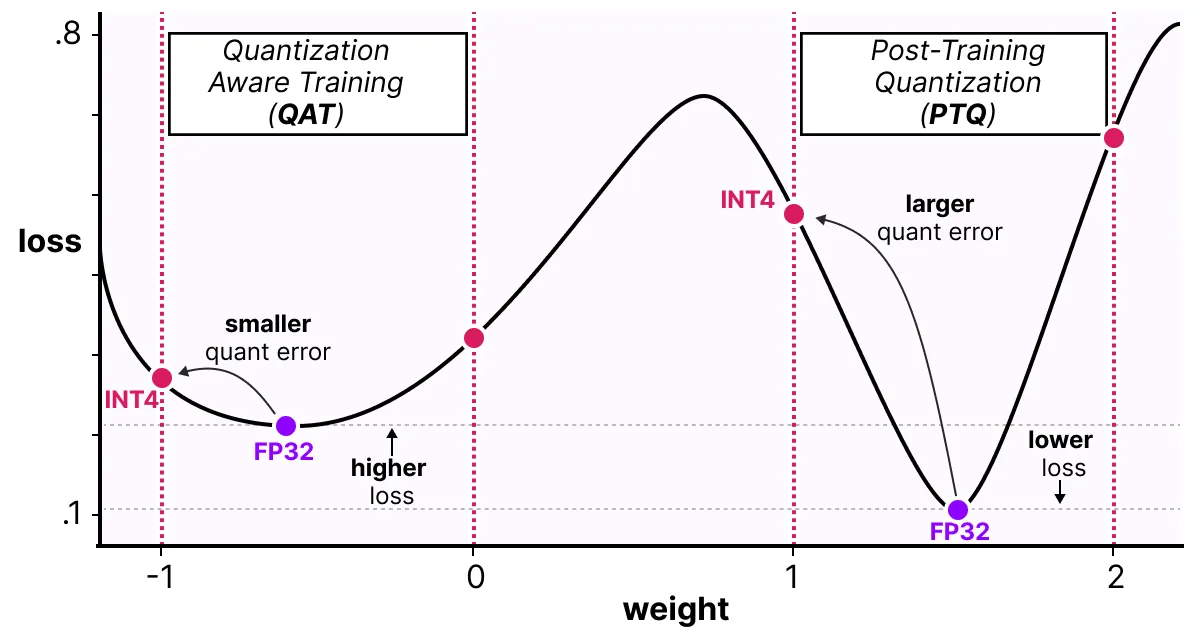
따라서, PTQ는 높은 정밀도(FP32 등)에서 더 낮은 손실을 보일 수 있지만, QAT는 낮은 정밀도(INT4 등)에서 더 낮은 손실을 초래하며, 이는 본래 목표로 하는 바이다.

The Era of 1-bit LLMs: BitNet

4비트로 모델을 경량화하는 것도 매우 작은 크기이지만, 더 압축하는 방법이 있다. 이를 위해 BitNet이 등장하였다. BitNet은 모델 가중치를 바이너리로 표현하며, -1 또는 1로서 단일 1비트로 변환한다. 이러한 양자화 과정을 Transformer 아키텍처에 직접적으로 적용하여 수행하는데, Transformer가 이미 LLM의 기본 아키텍처이기 때문에, 선형 레이어를 포함한 계산으로 구성되어 있음을 기억하면 좋다.

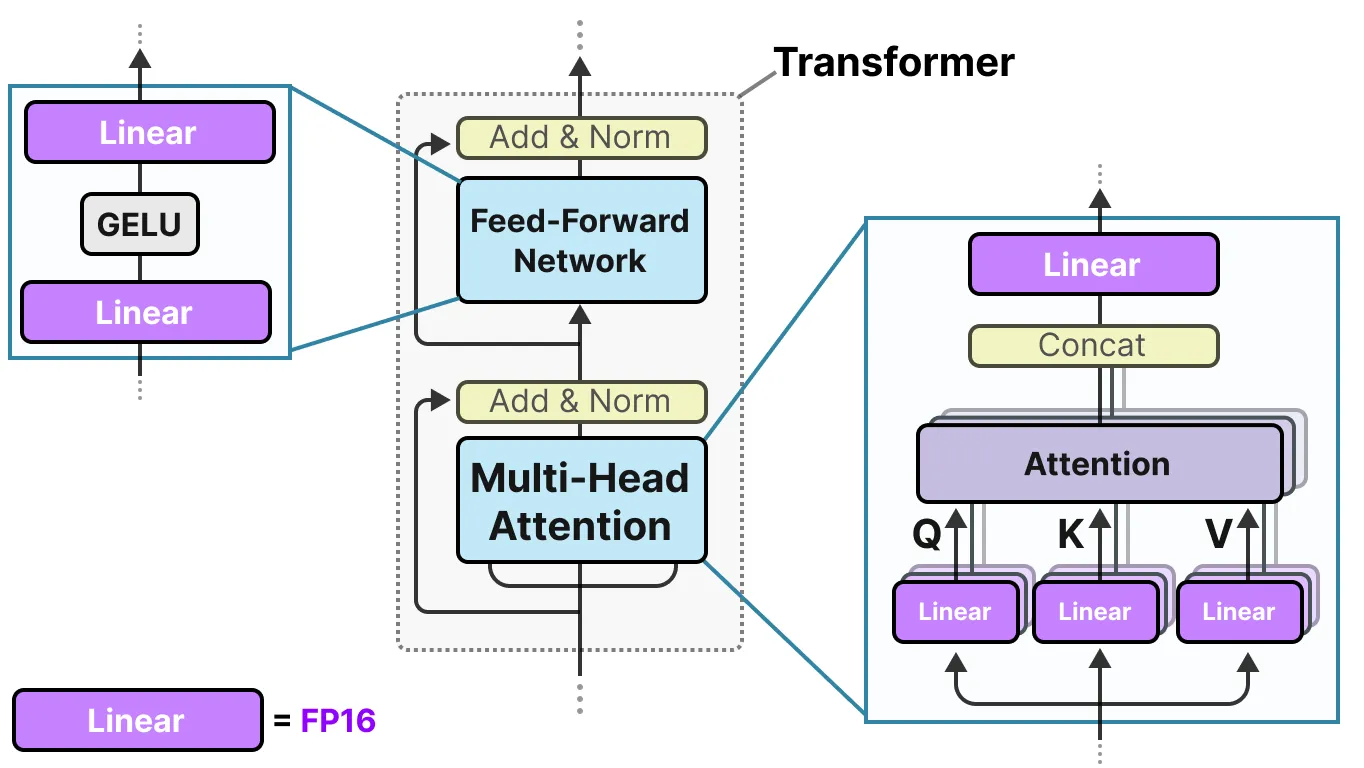
선형 레이어는 일반적으로 FP16과 같은 정밀도가 높은 수치 표현을 가진다. 그리고 대부분의 가중치가 있는 곳이다. BitNet은 이러한 선형 레이어를 BitLinear라는 구조로 대체한다.

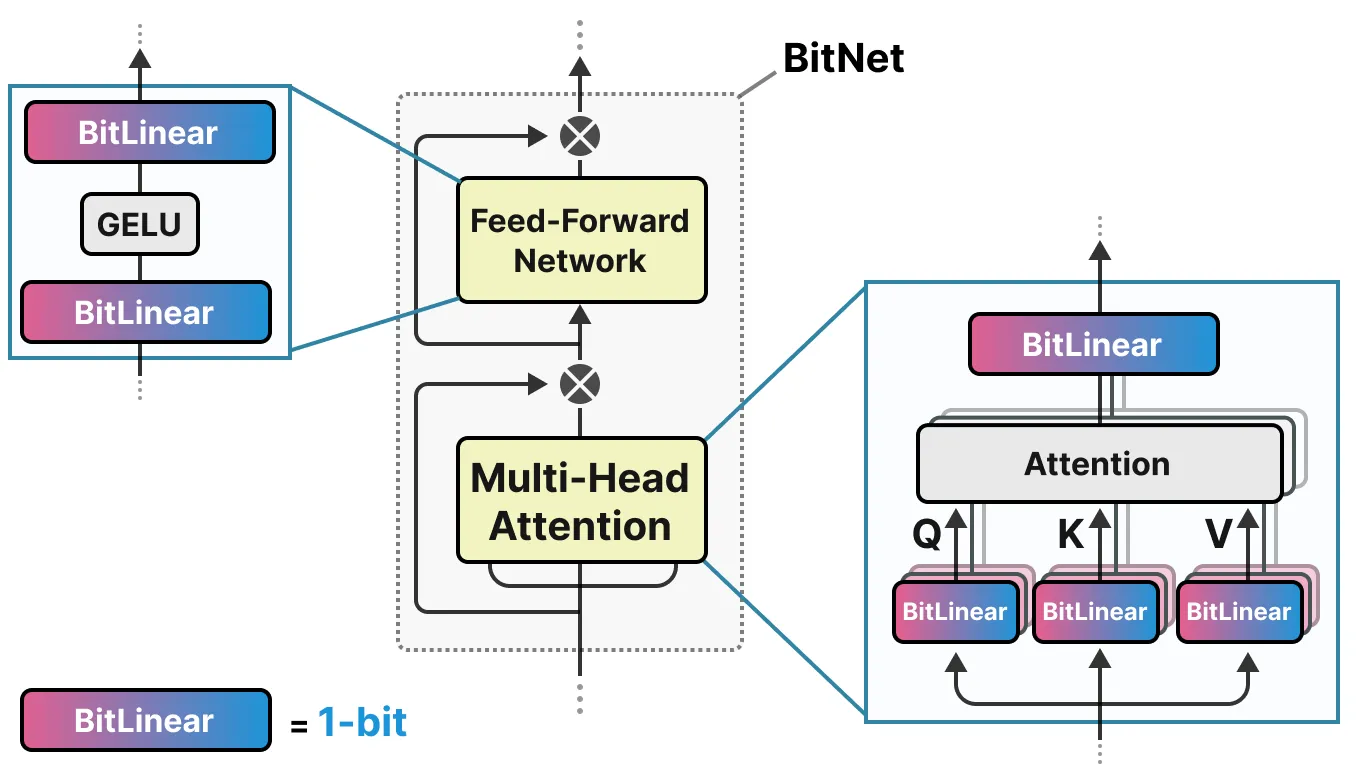
BitLinear 레이어는 일반적인 선형 레이어와 동일하게 작동하는데, 먼저 선형 레이어는 가중치에 활성화 값을 곱한 결과를 기반으로 출력을 계산한다. 반면 BitLinear 레이어는 1비트를 사용하여 모델의 가중치를 나타내며, INT8를 사용하여 활성화 값을 나타낸다.

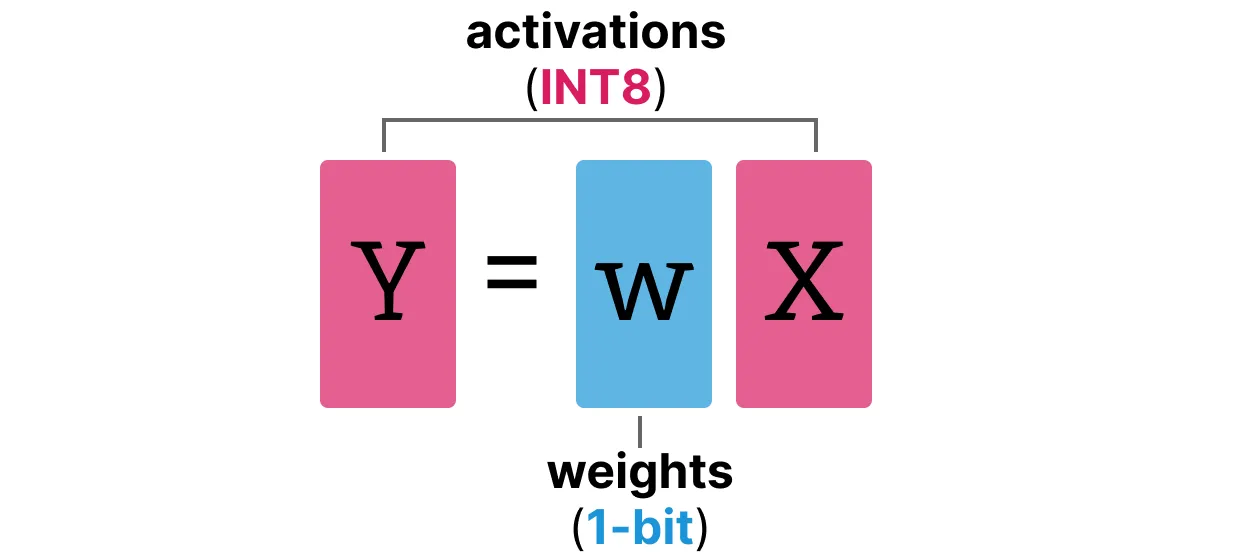
QAT와 같은 BitLinear 레이어는 훈련 중에 일종의 수도 양자화를 수행하여, 가중치와 활성화 값의 양자화 효과를 분석한다. 보다 자세히 BitLinear를 탐색해본다.

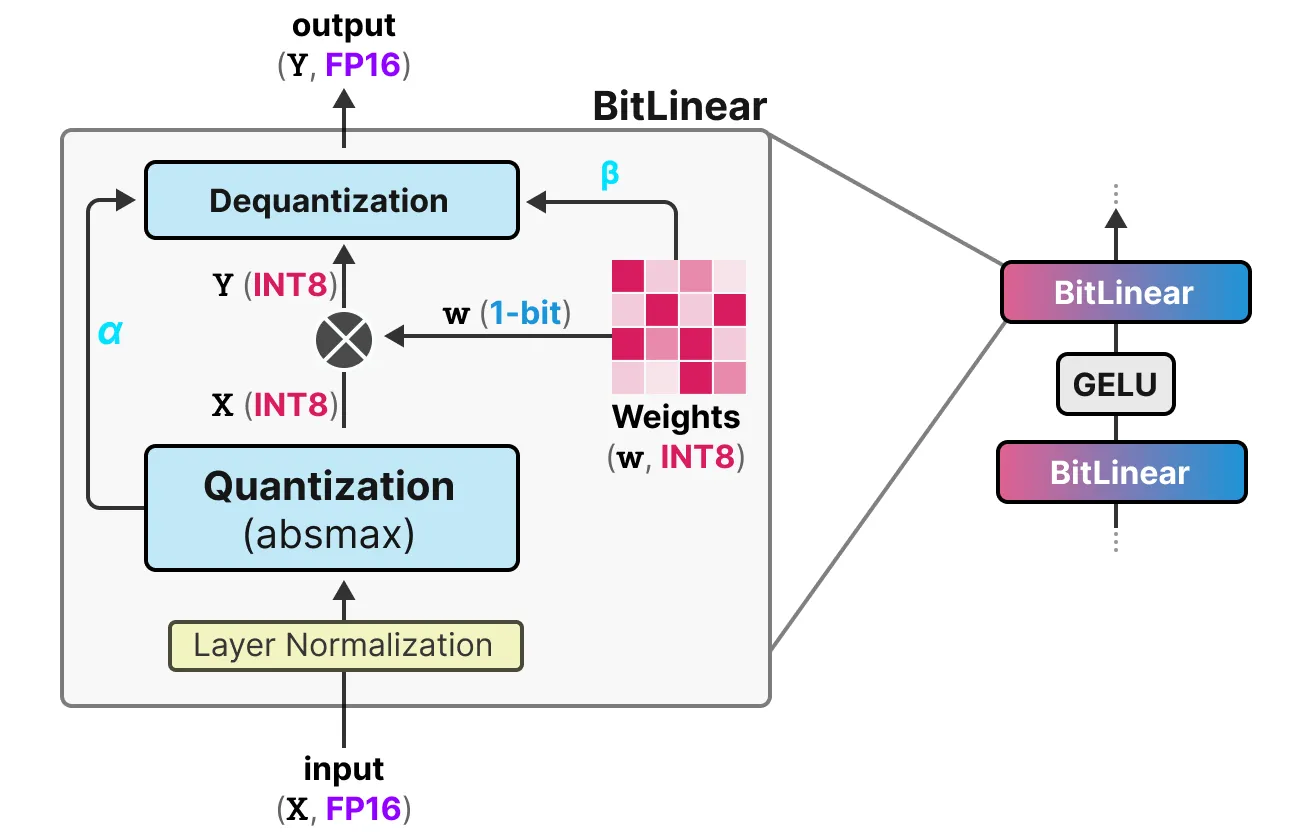
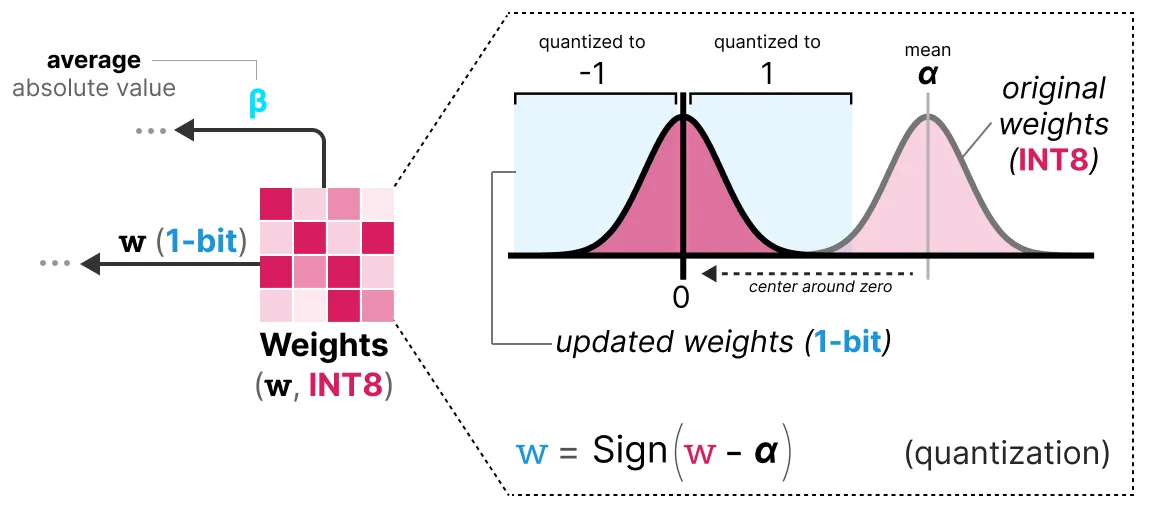
Weight Quantization

훈련 중에, 가중치는 INT8로 저장된 다음, signum function이라는 전략을 사용하여 1비트로 양자화 된다. 기본적으로 가중치 분포가 0을 중심으로 이동한 다음, 0의 왼쪽은 -1, 오른쪽은 1로 할당한다. 추가로 나중에 dequantization할때 사용할 beta(절대 평균) 값을 기록한다.

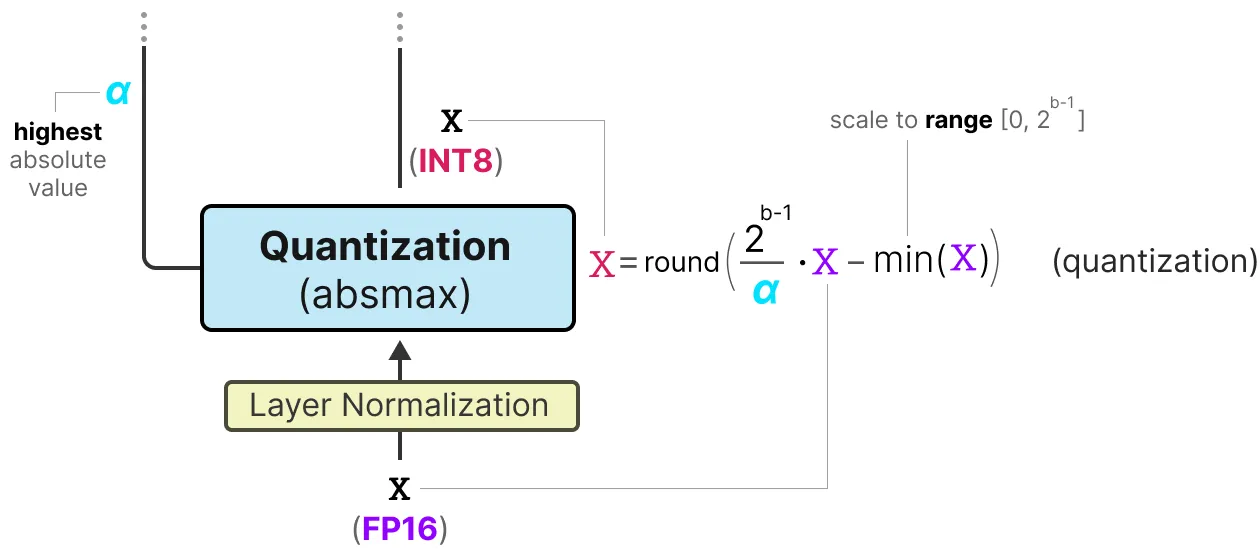
Activation Quantization

활성화 값을 양자화하려면, 행렬 곱셈을 위해 더 높은 정밀도가 필요하다. 따라서 BitLinear는 absmax 양자화를 사용하여 활성화 값을 FP16에서 INT8로 변환한다. 추가로 나중에 dequantization을 위해 alpha(가장 높은 절대값)을 기록한다.

Dequantization

alpha(가장 높은 절대값)과 beta(평균 절대값)은 활성화 값을 FP16으로 다시 양자화하는데 중요하므로 기록해야 한다. 출력 활성화 값은 원래의 정밀도로 dequantization된다.

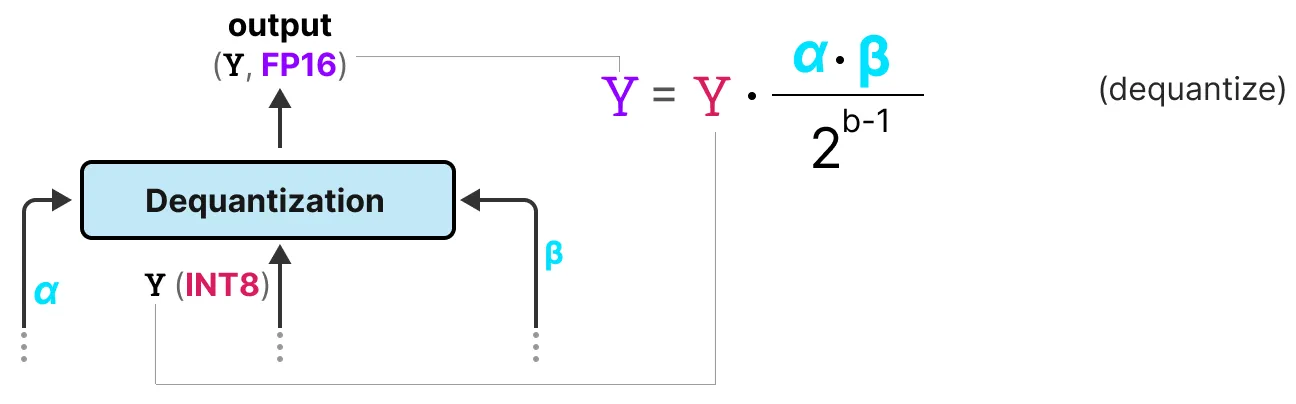
이 과정은 비교적 간단하며, [-1, 1] 값으로 모델을 표현한다. 저자들은 모델 크기가 커질수록 1비트와 FP16으로 훈련된 모델 간 성능 격차가 감소하는 것을 관찰하였다. 그러나 30B 이상의 대형 모델에서만 해당하며, 소형 모델과의 격차는 여전히 크다.

All Large Language Models are in 1.58 Bits

BitNet에서의 스케일링 문제를 개선하기 위해 BitNet 1.58b가 등장하였다. 이 방법은 모델의 모든 가중치가 [-1, 1] 말고 0 또한 값으로 포함 가능하여 삼항식이 되는 특징이 있다. 결과적으로 0만 추가하였는데, BitNet이 크게 개선되어 더 빠른 계산이 가능하다.

The Power of 0

왜 0을 더하는 것이 그렇게 큰 개선이 될까? 이는 행렬 곱셈과 연관이 있다. 출력을 계산하기 위해서는 가중치 행렬에 입력 벡터를 곱한다. 아래 그림에서 가중치 행렬의 첫 번째 레이어와 첫 번째 곱셈을 시각화 한 것이다.

이 곱셈에는 개별 가중치에 입력값을 곱한 다음 모두 더하는 두 가지 작업을 포함한다. 반면 BitNet 1.58b는 삼항 가중치가 다음의 의미를 담고 있다.

• 1: 해당 값을 더하고자 한다.
• 0: 해당 값을 원하지 않는다.
• -1: 해당 값을 빼고자 한다.

결과적으로 가중치가 1.58비트로 양자화된 경우에만 덧셈을 수행한다.

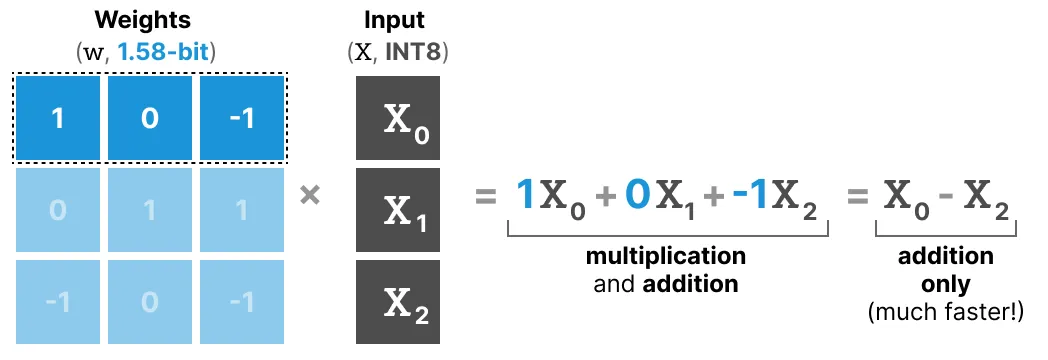
이 과정은 계산 속도가 빨라질 뿐만 아니라, 특징 필터링도 가능하다. 주어진 가중치를 0으로 설정하면 1비트 표현의 경우처럼 가중치를 더하거나 빼는 대신 무시할 수 있다.

Quantization

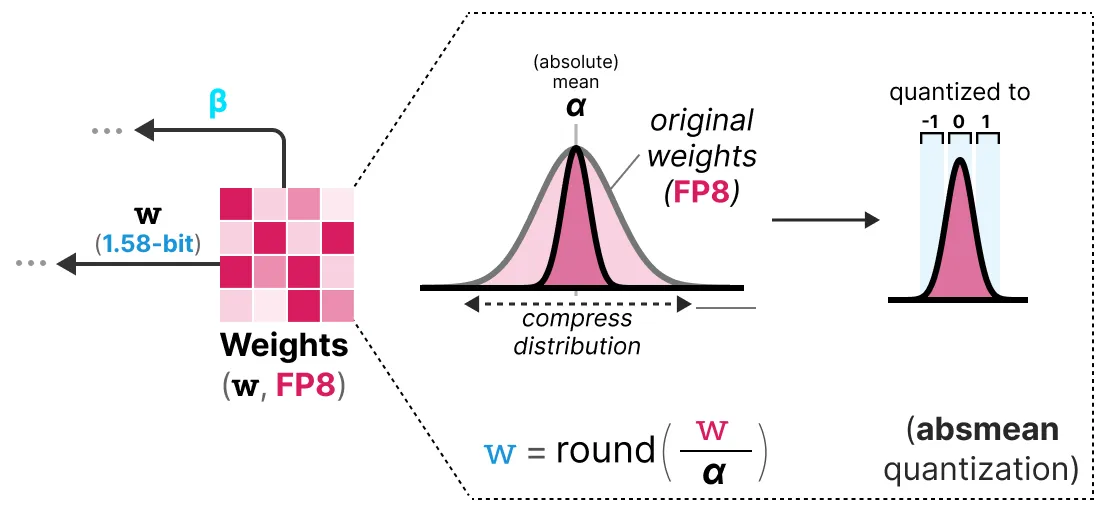
BitNet 1.58b는 가중치 양자화를 수행하기 위해 BitNet에서 사용한 absmax가 아니라, absmean 양자화를 사용한다. 이는 단순히 가중치 분포를 압축하고 alpha(절대 평균)을 사용해 값을 양자화 한다. 그런 다음 [-1, 0, 1]로 반올림한다.

BitNet과 비교했을때, 활성화 값 양자화는 한 가지를 제외하고 동일하다. 이제 활성화는 [0, 2ᵇ-¹] 범위로 스케일링되는 대신 absmax 양자화를 사용하여 [-2ᵇ-¹, 2ᵇ-¹]로 스케일링된다. 지연 시간, 메모리 사용량, 에너지 소비 측면에서 13B BitNet 1.58b가 3B FP16 LLM보다 더 효율적이다. 그 결과, 계산 효율이 1.58비트에 불과해 가벼운 모델을 만들 수 있다.

Conclusion

이 포스트는 GPTQ, GGUF, BitNet의 가능성을 다룬다. 이러한 기법들로 메모리 제약 조건을 극복하고 LLM이 더욱 경량화될 수 있는 발판을 마련할 수 있다. 더 많은 정보는 이 포스트의 원 저자와 Jay Alammar가 함께 쓰는 책이 있다.

Resources

저자는 다음의 레퍼런스를 추천한다.
[1] LLM.int8()
[2] Quantization Embedding
[3] Transformer Math
[4] GPTQ on YouTube
[5] Frantar, Elias, et al. “Gptq: Accurate post-training quantization for generative pre-trained transformers.” arXiv preprint arXiv:2210.17323 (2022).
[6] GGML repository
[7] Wang, Hongyu, et al. “Bitnet: Scaling 1-bit transformers for large language models.” arXiv preprint arXiv:2310.11453 (2023).
[8] Ma, Shuming, et al. “The era of 1-bit llms: All large language models are in 1.58 bits.” arXiv preprint arXiv:2402.17764 (2024).
[9] Dettmers, Tim, et al. “Qlora: Efficient finetuning of quantized llms.” Advances in Neural Information Processing Systems 36 (2023)